4

This question is very similar (but not identical) to this one:

Finding the distance between two gears

(actually, we are trying to solve it on Bicycle Exchange: https://bicycles.stackexchange.com/q/8608/2355)

The exact question is: "given two gears (pulleys, cilinders) with known radius, and a closed belt (chain, loop, rope) with known length (perimeter), how to calculate the maximum distance between the axles of the gears (that is, when they are pulled apart from each other)"?

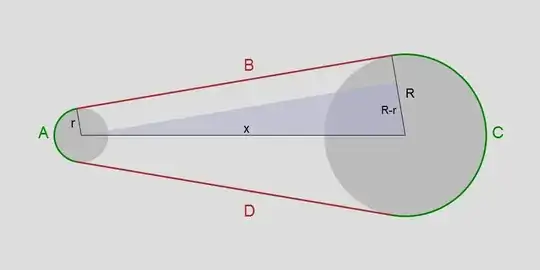
The ilustration: enter image description here

The equation we got so far:

$2B = L - R \left( \pi + 2\tan^{-1} \left( \frac{(R-r)}{B} \right) \right) - r \left( \pi - 2\tan^{-1} \left( \frac{(R-r)}{B} \right) \right)$

The main problem is that the unknown B appears on both sides and doesn't seem to be possible to isolate it.

Would it be possible to solve this problem algebrically, or only iteratively?

Community
  • 1
heltonbiker
  • 255
  • The equation you posted is not solvable algebrically. It is a transcendental equation. All you can get are approximate solutions. Using Maple, or other mathematical software, you should be able to solve for $B$ given $L,r,R$. – Beni Bogosel Mar 22 '12 at 20:24
  • Wow, that's exactely what I was wondering... Could you elaborate that in an answer so that I can accept it? – heltonbiker Mar 22 '12 at 21:01

1 Answers1

4

There is no closed form solution. I would add a reminder, eventually you probably want $$ x = \sqrt{B^2 + (R-r)^2} \; \; . $$

Just about the only thing that can be solved is an approximation, using a new letter $t$ with $0 < t < 1$ we have $$ \arctan t < t $$ and $$ \arctan t > t - \frac{t^3}{3}. $$ As we need $$ t = \frac{R - r}{B}, $$ the idea that $t < 1$ is the same as $R-r < B.$ I think this is a reasonable assumption.

So, the solvable approximation: replace $$ \arctan \left( \frac{R-r}{B} \right)$$ by $$ \left( \frac{R-r}{B} \right)$$ in your equation. Then multiply everything by $B.$ The result is a quadratic equation in $B,$ with solutions coming from the quadratic formula. If I were you, I would do this both in symbols and with some real life numbers, see how it goes. If a realistic true answer has $(R-r)/B < (1/10),$ I think you will be pleased with the approximation.

If the approximation is not quite good enough for your needs, it is still a good initial point for Newton's method, or any root-finding method...

Again, you probably want $$ x = \sqrt{B^2 + (R-r)^2} \; \; . $$

Will Jagy
  • 139,541
  • Thank you very much. Although I hadn't write it down, my need to find B is, actually, to use it in the right-rectangle formula you mentioned. B was the unknown left in the equation which contain every other known values (actually should be $L - 2B- R \left( \pi + 2atan \left( \frac{(R-r)}{B} \right) \right) - r \left( \pi - 2atan \left( \frac{(R-r)}{B} \right) \right) = 0$). Since I can program a numeric solution (python, javascript), I think I'll do it, but even so I'll consider your tips. Thanks again! – heltonbiker Mar 22 '12 at 21:21