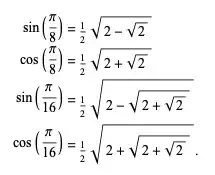Show that: $A_1A_2=R\sqrt{2-\sqrt{2+\sqrt{2-\sqrt{2+...+\sqrt{2}}}}}$ , the number of square roots being $n–1$.

Asked Apr 06 '21 at 10:48

Active Apr 08 '21 at 09:19

Viewed 121 times

Let $A_1A_2…A_k$ a polygone inscribed in a circle of radius $R$, with $k=2^n$ . Show that: $A_1A_2=R\sqrt{2-\sqrt{2+\sqrt{2-\sqrt{2+...+\sqrt{2}}}}}$ , the number of square roots being $n–1$. This may seem a nice problem By looking at this(If $ (A_1A_2)^2 + (A_1A_3)^2.......... + (A_1A_n)^2= 14r^2$, then prove that the number of sides is 7.) I deduced that $A_1A_{k+1}=2r\sin\Bigl(\frac{k\pi}{2^n}\Bigr)\ $ and so $A_1A_2=2R\sin(\frac{\pi}{2^n})$. I also observed that:

And such I deduce that $\sin(\frac{\pi}{2^n})$ would give me my desired squared root. It uses the formula of the division by $2$ of the argument of a trigonometric function in reverse and it gives me what I want. However, I don't know the inductive steps required and how to bridge my intuitive ideea to the general result in $n$. What my intuition says does not suffice. Any help, please?

edited Apr 08 '21 at 09:19

asked Apr 06 '21 at 10:48

1

Do you really mean $k=2n$ and not $k=2^n$? – ancient mathematician Apr 06 '21 at 11:00
1

See e.g. this https://math.stackexchange.com/a/85225/147873 – Winther Apr 06 '21 at 11:08
@ancientmathematician it is indeed as you observed. I have corrected – Apr 06 '21 at 13:01
@Winther I will try to write the answer immediately. – Apr 06 '21 at 13:02
1

Here and here you will find a few useful details that will help you with the square roots. – rtybase Apr 06 '21 at 13:11
1

You need the trig formulas $$2\cos\frac\alpha2=\pm\sqrt{2+2\cos\alpha}$$ and $$2\sin\frac\alpha2=\pm\sqrt{2-2\cos\alpha}$$ with the signs chosen according to the quadrant of $\alpha/2$. Convert a sine to a cosine of the complementary angle if/when required. Like here. – Jyrki Lahtonen Apr 06 '21 at 13:22

Show that: $A_1A_2=R\sqrt{2-\sqrt{2+\sqrt{2-\sqrt{2+...+\sqrt{2}}}}}$ , the number of square roots being $n–1$.

0 Answers0