0

I am trying to difference $ \sqrt {8x +1} $. When I use chain-rule I get $\frac{4}{\sqrt{8x+1}}$. I checked it in wolfram alpha and It is correct answer. But when I try to differentiate with limit, I came across with a problem. First, I write basic definition of derivatives:$$ \lim_{h \to 0} \frac{\sqrt{8(x+h) + 1} - \sqrt{8x + 1}}{h} $$ Then I multiply by $ \sqrt{8(x+h) + 1}$ and get: $$ \lim_{h \to 0} \frac{8(x+h) + 1 - \sqrt{8x + 1}\sqrt{8(x+h) + 1}}{h \sqrt{8(x+h) + 1}} $$ Then I assume that h in $\sqrt{8(x+h) + 1} \;$ equals $0$. (I think, this assumption is wrong, but I really don't know why? )$$ \lim_{h \to 0} \frac{8(x+h) + 1 - (8x + 1)}{h \sqrt{8x + 1}} $$At end I get$$ \lim_{h \to 0} \frac{8h}{h \sqrt{8x + 1}} = \frac{8}{\sqrt{8x + 1}}$$which is twice as much, as what I must get. My question is what I am getting wrong?

Nika Tvildiani
  • 101
  • 8
    Multiply by $\sqrt{8(x+h) + 1} + \sqrt{8x + 1}$ instead. – Arthur Mar 27 '21 at 20:04
  • 4
    Do what Arthur suggests. In your case you can't let $h=0$ in one part of the numerator and not the other. – John Douma Mar 27 '21 at 20:06
  • @JohnDouma So, that is general rule of assumption? – Nika Tvildiani Mar 27 '21 at 20:08
  • @NikaTvildiani If one copy is zero and the other is not then they cannot both be $h$. – John Douma Mar 27 '21 at 20:09
  • @JohnDouma OK, but then why can I assume only in numerator and left $h$ as it is in denominator? – Nika Tvildiani Mar 27 '21 at 20:11
  • You can't. If we can assume $h$ is zero in the numerator and not the denominator then every function is differentiable and has a derivative of zero. Why? – John Douma Mar 27 '21 at 20:14
  • @JohnDouma Now, when I use Arthur 's method, I understand. When it isn't $h$ left in nominator, we use assumption and really we use it in every part of equation. But still after it is crystal clear , it is fascinatingly strange, that using $h$ as zero in some places and as arbitrary very small number in other gives us completely different output. – Nika Tvildiani Mar 27 '21 at 20:29
  • 1
    On two occasions I have been asked, 'Pray, Mr. Babbage, if you put into the machine wrong figures, will the right answers come out?' I am not able rightly to apprehend the kind of confusion of ideas that could provoke such a question.

    Charles Babbage

     – John Douma Mar 27 '21 at 20:35
  • 1
    @NikaTvildiani: In truth, we are always talking about $h$ as it gets arbitrarily close to $0$, and never talking about what happens when $h=0$. When we write $\lim_{h \to 0}2x+h=2x$, what we are saying is that we can make $2x+h$ as close to $2x$ as we like by requiring that $h$ be sufficiently close to $0$. We are not saying that when $h=0$, $2x+h=2x$. Nevertheless, plugging in $h=0$ still works... – Joe Mar 27 '21 at 20:37
  • 1
    ...The reason that it works is because polynomial functions are continuous: they have the property that $\lim_{x \to a}f(x)=f(a)$ for all $a$—in other words, the limiting value is the same as the value that you get when you plug in $x=a$. Not all classes of functions are so well-behaved. – Joe Mar 27 '21 at 20:37
  • When you make mistake, you always trying to find why you make it and find way to avoid it. So, now I am minding , how I should have figured it out, that I must have multiplied by what Arthur suggested and not what I multiplied it by. Or that making assumption only in one part of equation is wrong. I always wonder, If there general algorithm or formula for such decisions. But I think, It is bit off topic and more general question, may be even more philosophical. – Nika Tvildiani Mar 27 '21 at 20:46
  • @NikaTvildiani: Does my last comment help clear up some of your confusions? In any case, I am writing a longer answer right now. – Joe Mar 27 '21 at 20:48
  • Yes, It quiet helped. I remember reading about limits and derivatives in Grigorii Fichtenholz book. But It was years ago and then I was starting getting know with advance Math. In such books there are many examples, with very clever tricks to solve specific derivatives. But they sometimes lack of explanation. They not saying why using this or that tool. They just say to use it because they work. Sometimes, I think they just use many of them and one worked out. So, is there general method to find out in advance which method to use... – Nika Tvildiani Mar 27 '21 at 20:56
  • @NikaTvildiani: The short answer is no, sadly. The answer which I am about to post is mostly there to reinforce your conceptual understanding, rather than helping you solve these problems. The best way to get good and doing limits is to solve lots of practice problems. – Joe Mar 27 '21 at 21:56

1 Answers1

2

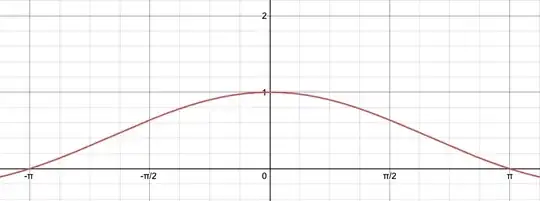
In general, when you have to compute $$ \lim_{h \to 0}\frac{f(x+h)-f(x)}{h} \, , $$ you are not allowed to simply set $h$ equal to $0$ without thinking. This is because limits tell you what a function does as $h$ gets close to $0$, but is not equal to it. Consider the graph of $y=\frac{\sin h}{h}$, where $h$ is measured in radians:

Graph of sin h /h

Looking at this plot, it is clear that as $h$ gets very close to $0$, $\frac{\sin h}{h}$ also gets very close to $1$. The graph seems to suggest that $$ \frac{\sin 0}{0}=1 \, , $$ even though that is complete nonesense. Actually, the function is not defined when $h=0$. Nevertheless, we retain a strong urge to talk about the behaviour of the function around that point. Limits allow us to do this. When we write $$ \lim_{h \to 0}\frac{\sin h}{h}=1 \, , $$ what we mean is that $\frac{\sin h}{h}$ gets arbitrarily close to $1$ as $h$ approaches $0$. Although the function $\frac{\sin h}{h}$ never attains the value of $1$, the value of $1$ is the 'anticipated' value.

More formally, the expression $$ \lim_{h \to 0}\frac{\sin h}{h}=1 $$ is a shorthand for

We can make $\frac{\sin h}{h}$ as close to $1$ as we like by requiring that $h$ be sufficiently close to, but unequal to, $0$.

You might need to re-read that last sentence a few times. It is practically the definition of a limit, and I'm not exaggerating when I say that this definition forms the bedrock of the theory behind calculus.

Notice that the definition of a limit explicitly states that we are looking at the behaviour of a function around $0$, not at $0$. Even if a function is defined at $0$, this is still entirely irrelevant. For instance, consider the function $f$ given by $$ f(x) = \begin{cases} 2x &\text{ if $x\neq0$} \\ 42 &\text{ if $x=0$} \, . \end{cases} $$ It is clear that as $x$ shrinks towards $0$, so does $2x$. Hence, $$ \lim_{x \to 0}f(x)=0 \, . $$ This is in spite of the fact that $f(0)=42$.

However, there are still many cases where plugging in the value being approached does work. Consider, for instance, the limit as $h$ approaches $0$ of $2x+h$. This limit is equal to $2x$, and we could got this answer by naively plugging in $h=0$. Functions like this are said to be continuous. In general, a function $f$ is said to be continuous at the point $a$ if $$ \lim_{x \to a}f(x)=f(a) \, . $$ As it turns out, almost all of the functions you are familiar have this property. This includes:

  • Polynomials and rational functions (quotients of polynomials)
  • Trigonometric and hyperbolic functions, and their inverses
  • Exponential and logarithmic functions

And all of the functions you get as a result of adding, multiplying, or composing the above functions.

This means when we consider the limit of one of these functions, then provided that they are defined there, simply plugging in the value being approached does work. This is the reason that the users in the comments are suggesting that you transform your problem into something where you alllowed to simply plug in $h=0$ into the entire expression. This method works precisely because the functions that you are used to dealing with—the elementary functions—are continuous.

There are people who have written about this in the past on this site, and have done so much more concisely than I could manage. I would suggest that you look at the following threads:

Joe
  • 19,636