Evaluating $\int_{-1}^{1}\frac{\arctan{x}}{1+x}\ln{\left(\frac{1+x^2}{2}\right)}dx$

Question

This is a nice problem. I am trying to use nice methods to solve this integral, But I failed.

$$\int_{-1}^{1}\dfrac{\arctan{x}}{1+x}\ln{\left(\dfrac{1+x^2}{2}\right)}dx, $$

where $\arctan{x}=\tan^{-1}{x}$

mark: this integral is my favorite one. Thanks to whoever has nice methods.

I have proved the following:

$$\int_{-1}^{1}\dfrac{\arctan{x}}{1+x}\ln{\left(\dfrac{1+x^2}{2}\right)}dx=\sum_{n=1}^{\infty}\dfrac{2^{n-1}H^2_{n-1}}{nC_{2n}^{n}}=\dfrac{\pi^3}{96}$$

where $$C_{m}^{n}=\dfrac{m}{(m-n)!n!},H_{n}=1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n}$$

I also have got a few by-products $$\int_{-1}^{1}\dfrac{\arctan{x}}{1+x}\ln{\left(\dfrac{1+x^2}{2}\right)}dx=-I_{1}-2I_{2}$$

where $$I_{1}=\int_{0}^{1}\dfrac{\ln{(1-x^2)}}{1+x^2}\ln{\left(\dfrac{1+x^2}{2}\right)}dx=\dfrac{\pi}{4}\ln^2{2}+\dfrac{\pi^3}{32}-2K\times\ln{2}$$

and $$I_{2}=\int_{0}^{1}\dfrac{x\arctan{x}}{1+x^2}\ln{(1-x^2)}dx=-\dfrac{\pi^3}{48}-\dfrac{\pi}{8}\ln^2{2}+K\times\ln{2}$$

and same methods,I have follow integral $$\int_{0}^{1}\dfrac{\ln{(1-x^4)}\ln{x}}{1+x^2}dx=\dfrac{\pi^3}{16}-3K\times\ln{2}$$ where $ K $ denotes Catalan's Constant.

Answer 1

Here is a solution that only uses complex analysis:

Let $\epsilon$ > 0 and consider the truncated integral

$$ I_{\epsilon} = \int_{-1+\epsilon}^{1} \frac{\arctan x}{x+1} \log\left( \frac{1+x^2}{2} \right) \, dx. $$

By using the formula

$$ \arctan x = \frac{1}{2i} \log \left( \frac{1 + ix}{1 - ix} \right) = \frac{1}{2i} \left\{ \log \left( \frac{1+ix}{\sqrt{2}} \right) - \log \left( \frac{1-ix}{\sqrt{2}} \right) \right\}, $$

it follows that

$$ I_{\epsilon} = \Im \int_{-1+\epsilon}^{1} \frac{1}{x+1} \log^{2} \left( \frac{1+ix}{\sqrt{2}} \right) \, dx. $$

Now let $\omega = e^{i\pi/4}$ and make the change of variable $z = \frac{1+ix}{\sqrt{2}}$ to obtain

$$ I_{\epsilon} = \Im \int_{L_{\epsilon}} \frac{\log^2 z}{z - \bar{\omega}} \, dz, $$

where $L_{\epsilon}$ is the line segment joining from $\bar{\omega}_{\epsilon} := \bar{\omega} + \frac{i\epsilon}{\sqrt{2}}$ to $\omega$. Now we tweak this contour of integration according to the following picture:

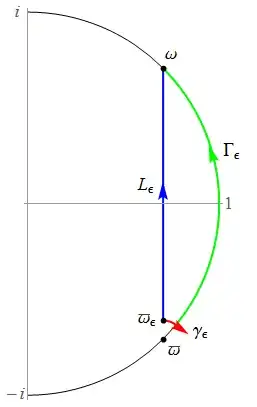
That is, we first draw a clockwise circular arc $\gamma_{\epsilon}$ centered at $\bar{\omega}$ joining from $\bar{\omega}_{\epsilon}$ to some points on the unit circle, and draw a counter-clockwise circular arc $\Gamma_{\epsilon}$ joining from the endpoint of $\gamma_{\epsilon}$ to $\omega$. Then

$$ I_{\epsilon} = \Im \int_{\gamma_{\epsilon}} \frac{\log^2 z}{z - \bar{\omega}} \, dz + \Im \int_{\Gamma_{\epsilon}} \frac{\log^2 z}{z - \bar{\omega}} \, dz =: J_{\epsilon} + K_{\epsilon}. $$

It is easy to check that as $\epsilon \to 0^{+}$, the central angle of $\gamma_{\epsilon}$ converges to $\pi / 4$. Since $\gamma_{\epsilon}$ winds $\bar{\omega}$ clockwise, we have

$$ \lim_{\epsilon \to 0^{+}} J_{\epsilon} = \Im \left( -\frac{i \pi}{4} \mathrm{Res}_{z=\bar{\omega}} \frac{\log^2 z}{z - \bar{\omega}} \right) = \frac{3}{2} \frac{\pi^3}{96}. $$

Also, by applying the change of variable $z = e^{i\theta}$,

$$ K_{\epsilon} = -\Re \int_{-\frac{\pi}{4}+o(1)}^{\frac{\pi}{4}} \frac{\theta^2}{1 - \bar{\omega}e^{-i\theta}} \, d\theta = \int_{-\frac{\pi}{4}+o(1)}^{\frac{\pi}{4}} \frac{\theta^2}{2} \, d\theta. $$

Thus taking $\epsilon \to 0^{+}$, we have

$$ \lim_{\epsilon \to 0^{+}} K_{\epsilon} = - \int_{0}^{\frac{\pi}{4}} \theta^2 \, d\theta = - \frac{1}{2} \frac{\pi^3}{96}. $$

Combining these results, we have

$$ \int_{-1}^{1} \frac{\arctan x}{x+1} \log \left( \frac{x^2 + 1}{2} \right) \, dx = \frac{\pi^3}{96}. $$

The same technique shows that

$$ \int_{-1}^{1} \frac{\arctan (t x)}{x+1} \log \left( \frac{1 + x^2 t^2}{1 + t^2} \right) \, dx = \frac{2}{3} \arctan^{3} t, \quad t \in \Bbb{R} .$$

Answer 2

FWIW, here's Maple:

> f:= arctan(x)/(1+x)*ln((1+x^2)/2);
> int(f, x=-1..1);

$$ {\frac {7}{64}}\,{\pi }^{3}-{\frac {5}{16}}\,\pi \, \left( \ln \left( 2 \right) \right) ^{2}-\ln \left( 2 \right) {\it Catalan}+1/ 2\, \left( \ln \left( 1-i \right) \right) ^{2}\pi -1/2\,i \left( \ln \left( 1+i \right) \right) ^{2}\ln \left( 2 \right) +\ln \left( 1+i \right) {\it Catalan}+1/2\, \left( \ln \left( 1+i \right) \right) ^{2}\pi -i{\it polylog} \left( 3,-i \right) +i{\it polylog} \left( 3,i \right) +1/2\,i \left( \ln \left( 1-i \right) \right) ^{2}\ln \left( 2 \right) -1/2\,i \left( \ln \left( 1-i \right) \right) ^{3}-1/48\,i\ln \left( 1+i \right) {\pi }^{2}+1/2\, i \left( \ln \left( 1+i \right) \right) ^{3}+\ln \left( 1-i \right) {\it Catalan}+1/48\,i\ln \left( 1-i \right) {\pi }^{2} $$

> simplify(%);

$$ \frac{\pi^3}{96} $$

I don't know if that qualifies as "nice", but it's certainly easy.

Answer 3

Splitting the integral at $x=0$, letting $x\mapsto -x$ in the first integral and then adding it to the second one, we arrive at $$\int_{-1}^1\frac{\arctan(x)\log((1+x^2)/2)}{1+x}\textrm{d}x=2\int_0^1 \frac{x\arctan(x) \log(2/(1+x^2))}{1-x^2}\textrm{d}x=\frac{\pi^3}{96},$$ where the last integral is extracted in this solution magically exploiting the symmetry of a triple integral.

End of story