1

I've heard many times of functions that cannot be integrated. For example, $x^x$, which is the most common. But what I don't know is how could you, even if the graph has no equation, plot this integral. If anyone could give me a graph, I would be extremely pleased. Or at least, could you tell me how to graph it? Maybe in Wolfram Mathematica?

Anonymous Pi
  • 1,297
  • 1
    It is not true that $x^x$ cannot be integrated: where defined, the function is continuous, which means that it is Riemann integrable there. Instead, what you're probably thinking of is that $x^x$ has no elementary antiderivative, ie there is no elementary function $g$ such that $g'=x^x$. – KReiser May 30 '13 at 20:19
  • It's false that $x^x$ "cannot be integrated", it's just that its integral cannot be expressed in terms of elementary functions. Why are you interesetd in its graph? – leonbloy May 30 '13 at 20:20
  • The same way you graph the solution of any ordinary differential equation for which you are unable to write an explicit solution: solve numerically to some accuracy over some interval, say $0 < x < 3.$ You might as well take $y(0) = 0,$ it does no harm. I see, @Raymond has done that in an answer, with $0 < x < 2$ – Will Jagy May 30 '13 at 20:33
  • 1
    I don't think this is a duplicate as such, since it is specifically looking for a graph, which the other question did not provide. – Ben Millwood May 30 '13 at 20:46
  • Thanks @KReiser, but I already understand that x^x can not be expressed in terms of elementary functions. However, by taking your g'=x^x example, do you know how could I graph g? – Anonymous Pi Jun 03 '13 at 16:08

3 Answers3

3

Here is a quick picture of $\ x\mapsto \int_0^x t^t\;dt$

plot

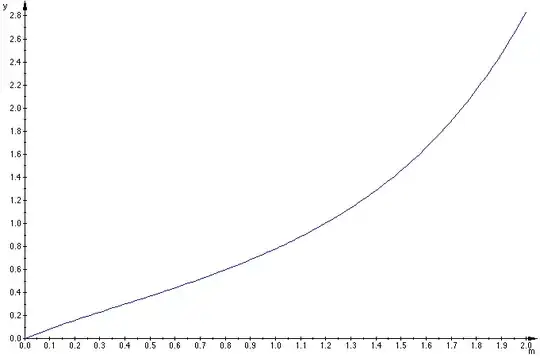
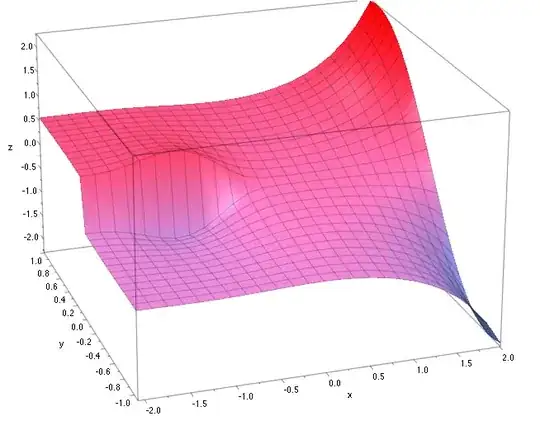
I added the plot of the real and imaginary part of the integral in the complex plane $\ z\mapsto \int_0^z t^t\;dt\ $ with $z=x+iy$ (note the 'branch jump' on the negative axis $(-\infty,0)$).

real part of the integral

imaginary part

Raymond Manzoni
  • 43,021
  • 5
  • 86
  • 140
  • The values $I(0)=0,\ I(1)\approx 0.7834305107,\ I(2)\approx 2.833876745$ (I am computing the integral...) – Raymond Manzoni May 30 '13 at 20:28
  • These may be compared to the values provided in the famous "Sophomore's Dream". – Raymond Manzoni May 30 '13 at 20:31
  • Did you use Wolfram Mathematica?

    And also, do you know how could I find the Taylor series of this graph? (I am kind of a beginner in these kinds of things)

     – Anonymous Pi Jun 03 '13 at 16:09
  • @AnonymousPi: I used MuPad (recent versions of MatLab incorporates this CAS too) and asked directly to plot the numerical integral of $x^x$. You may rewrite $x^x=e^{x\ln(x)}$ to get the expansion proposed by Mhenni and then integrate every term $\int (x\ln(x))^n;dx=$ as done by Alpha (replace $n$ by small integers) but this is rather laborious and not really a Taylor series because of the $\log$ terms... The other thread should really help you more! – Raymond Manzoni Jun 03 '13 at 21:01
1

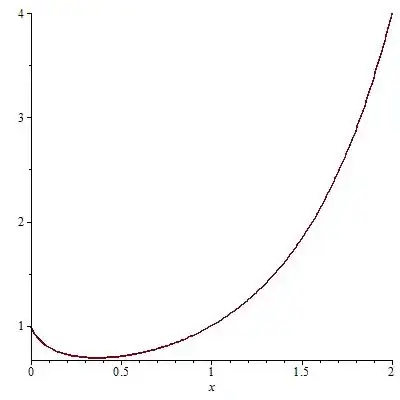
Here is the graph of the function with Maple

Plot( $x^x$, $x=0..2$ );

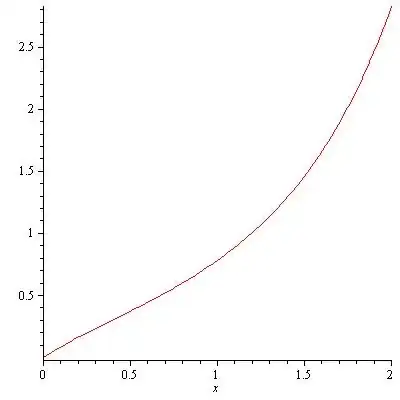
enter image description here

The graph of the integral of $x^x$ using the truncated Taylor series

$$ x^x=1+\ln \left( x \right) x+\frac{1}{2}\, \left( \ln \left( x \right) \right) ^{2}{x}^{2}+\frac{1}{6}\, \left( \ln \left( x \right) \right) ^{3}{x}^{3}+\frac{1}{ 24}\, \left( \ln \left( x \right) \right) ^{4}{x}^{4}+O(x^5). $$

enter image description here

Mhenni Benghorbal
  • 47,431
1

Here is an interesting thread for you: http://www.physicsforums.com/showthread.php?t=77605

Quote: The integral of x^x between 0 and 1 was calculated by Johann Bernoulli in 1697 using power series (not Euler). The proof appears in "Opera Omnia" vol. 3 (1697) pp. 376 - 381.

Armin Meisterhirn
  • 403