My general question is very vague, so before let's look at the following example. Fix $n\in\mathbb{N}$ and consider a family of polynomials $p_a (z) = (az+1)^n - \dfrac{z^{n+1}-1}{z-1}$ for $a\in\mathbb{R}$ and $z\in\mathbb{C}$. Here we view $a$ as a parameter of a family.
Let's fix $n\in\mathbb{N}$ large enough ($n=50$) and draw the sets of roots of $p_a(z)$ for some $a$'s.
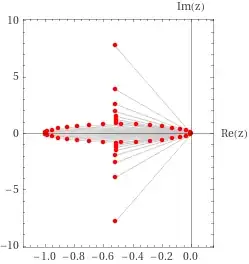
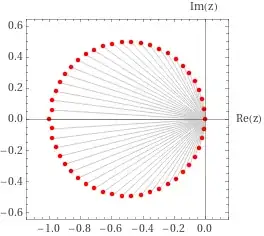
For $a=1$ we have
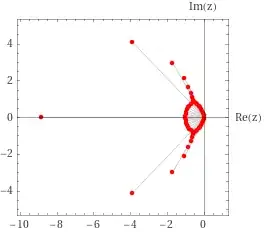
For $a=\dfrac{10}9$:
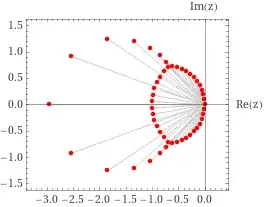
For $a=\dfrac{12}9$:
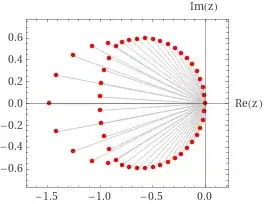
For $a=\dfrac{15}9$:
For $a=2$:
First, when $a=1$ the roots lie near the circle and the $\Re =-\dfrac12$ line. As $a$ increases the line transforms into another circle and finally the two circles merge. For $a>2$ nothing new happens. If one instead decreases $a$ then the second circle forms analogously. The exact same pattern holds for any bigger $n$.
Now, in this particular example I do understand why any of this happens and my question is more general:
Is there any theory that studies topology of zero sets for parametrized families of polynomials?
I'm not really sure what I precisely mean by topology in this case as the set of roots is discrete. Maybe some approximation by removing all the balls from $\mathbb{C}$ of fixed radius that do not intersect the set of roots. By varying the radius of such balls we will get different approximation.