How to get the area of the triangle inscribed in the unit circle when a slope is tangent?

Question

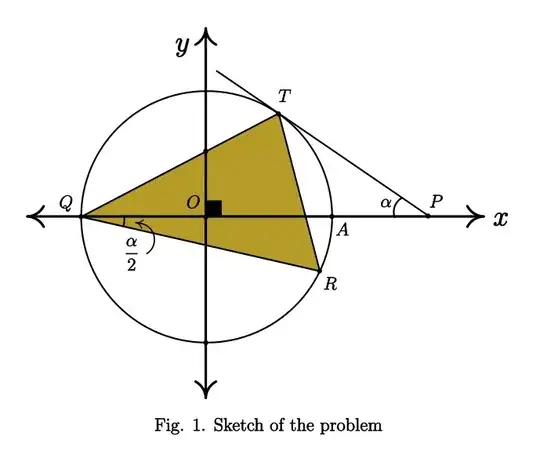
The problem is as follows:

The circle shown in the figure from below is a unit circle. $PT$ is a line tangent to that circle on point $T$. Angle alpha measured in radians is an acute angle. Using this information, find the area of the orange shaded region which is comprised $\triangle TQR$. Assume that the length of the radius of the unit circle is of 1 decameter.

The choices given in my book are as follows:

$\begin{array}{ll} 1.&200\cos\alpha\sin\left(\frac{\pi}{6}-\frac{\alpha}{2}\right)\\ 2.&100\sqrt{2}\cos\frac{\alpha}{2}\sin\left(\frac{\pi}{4}-\frac{\alpha}{2}\right)\\ 3.&50\sin\alpha\sin\left(\frac{\pi}{4}-\frac{\alpha}{2}\right)\\ 4.&100\sqrt{2}\sin\frac{\alpha}{2}\sin(45^\circ+\alpha)\\ \end{array}$

I'm not sure exactly how to solve this question, it seems kind of difficult to my abilities.

I tried all sorts of manipulations on the image but I can't find a proper relation to get the base of the triangle. I also considered the oportunity to use the tangent secant theorem but this did not helped me much in the solution.

This half angle thing which is on the third quadrant it is making me feel confused. Needless to say that it is more than thirty minutes and I don't think I am getting anywhere with this problem.

Can someone help me here?.

I am totally lost here. Since I'm not good at spotting things it would help a lot that a drawing could accompany the solution as I guess that it is needed some labels to see where should additional or rearranging the angles would be needed to solve this problem.

Answer 1

Add lines OT and OR. Notice that $\triangle OTA$ is a right triangle. Then you have $$|\sphericalangle TOA| = 90^\circ - \alpha$$ $$|\sphericalangle TQA| = \frac12|\sphericalangle TOA| = 45^\circ - \frac{\alpha}{2}$$ Then you should be able to find all the angles in the picture. Eventually you should get $$|\sphericalangle TOQ| = 90^\circ+\alpha$$ $$|\sphericalangle TOR| = 90^\circ$$ $$|\sphericalangle QOR| = 180^\circ-\alpha$$ We have then \begin{align} S(\triangle TQR) &= S(\triangle TOQ)+ S(\triangle TOR) + S(\triangle QOR) = \\ &= \frac12 10^2(\sin|\sphericalangle TOQ| + \sin|\sphericalangle TOR| + \sin|\sphericalangle QOR|) = \\ &= 50\big(\sin(90^\circ+\alpha) + 1 + \sin(180^\circ-\alpha)\big) \end{align}

After some trigonometry you can show that it's equal to $$ 100\sqrt{2}\cos\frac{\alpha}{2}\sin\big(45^\circ+\frac{\alpha}{2}\big) $$

Strangely enough, it's neither of the answers you can choose from, but you can also find $$|\sphericalangle TQR| = 45^\circ$$ $$|\sphericalangle QRT| = 45^\circ+\frac{\alpha}{2}$$ $$|\sphericalangle RTQ| = 90^\circ-\frac{\alpha}{2}$$ There is a well-known formula that links the radius of the circumscribed circle to the lengths of the sides and angles of the triangle: $$ 2R = \frac{|TR|}{\sin|\sphericalangle TQR|} = \frac{|QT|}{\sin|\sphericalangle QRT|} = \frac{|RQ|}{\sin|\sphericalangle RTQ|} $$ We have then $$ |TR| = 2R \sin |\sphericalangle TQR|$$ $$ |QT| = 2R \sin |\sphericalangle QRT|$$ \begin{align} S(\triangle TQR) &= \frac12 R^2\, |TR| |QT| \sin|\sphericalangle RTQ| = \\ &= 2R^2 \sin|\sphericalangle TQR| \sin|\sphericalangle QRT| \sin|\sphericalangle RTQ| = \\ &= 200 \cdot \frac{\sqrt{2}}{2} \sin\big(45^\circ+\frac{\alpha}{2}\big) \sin\big(90^\circ-\frac{\alpha}{2}\big) = \\ &= 100\sqrt{2} \sin\big(45^\circ+\frac{\alpha}{2}\big) \cos\frac{\alpha}{2}\end{align} and we get the same result.

Answer 2

Coordinate of $Q$ is $(-1, 0)$.

Since $\angle AOR = \alpha$, coordinate of $R$ is $(\cos \alpha, -\sin \alpha)$.

Since $\angle TOA = \frac{\pi}{2}-\alpha$, coordinate of $T$ is $\left( \cos\left(\frac{\pi}{2}-\alpha\right), \sin \left( \frac{\pi}{2}-\alpha \right) \right)=(\sin \alpha, \cos \alpha)$.

The corresponding area is

\begin{align} \frac12 \cdot 100 \cdot \begin{vmatrix} -1 & \cos \alpha & \sin \alpha \\ 0 & -\sin \alpha & \cos \alpha \\ 1 & 1 & 1\end{vmatrix} &= 50 \cdot (\sin \alpha + \cos \alpha + \cos^2 \alpha +\sin^2 \alpha) \\ &= 50 \cdot \left[(1 + \sqrt2 \sin \left(\alpha + \frac\pi4 \right)\right] \\ &= 50 \sqrt{2}\left[\sin\left( \frac{\pi}{4} \right) + \sin \left( \alpha + \frac{\pi}4\right)\right] \\ &= 100 \sqrt2 \cos \left( \frac{\alpha}2\right)\sin \left( \frac{\alpha}2\color{red}+\frac{\pi}4\right) \end{align}