Relationships between $2$ mutually tangent circles in a semi-circle

Question

In the attempt to answer this question, I was brought to another one, connected to a certain family of circles.

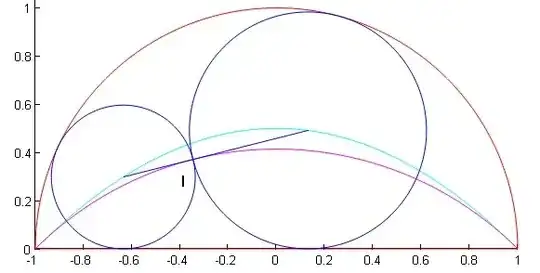
Consider the semicircle made of the upper half of the unit circle and the horizontal diameter with endpoints $A(-1,0)$ and $B(1,0)$.

Let us now consider the family $(F)$ of circles inscribed into this semicircle as can be seen on Fig. 1.

Fig. 1: Certain circles of family $(F).$

They can be described in a parametric way as circles

$$\text{with center} \ (x_c=-\cos a, y_c=\frac12 \sin^2a) \ \text{and radius} \ y_c, \ a \in (0,\pi) \tag{1}$$

or equivalently as circles $(C_T)$

$$\text{with center} \ \left(x_c=\frac{T^2-1}{(1+T)^2}, y_c=\frac{2T}{(1+T)^2}\right) \ \text{and radius} \ y_c, \ T \in (0,+\infty) \tag{2}$$

(Connection between the two parameterizations: $T=t^2$ where $t:=\tan \tfrac{a}{2}$).

The locus of these centers is parabola $(P)$ with cartesian equation:

$$y=\tfrac12(1-x^2),\tag{3}$$

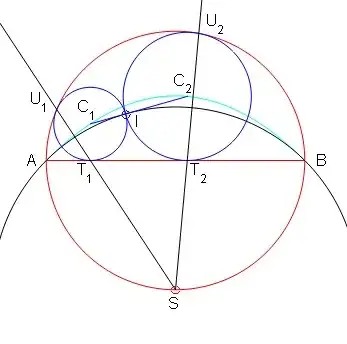
represented on Fig. 2 as the light blue curve.

Each circle $(C_T) \in F$ is associated with a unique circle $(C_{T'}) \in F$ which is tangent to $(C)$ as depicted on Fig. 2.

Fig. 2: Two circles of family $(F)$ are mutually tangent if their parameters $T$ and $T'$ comply with relationship (4).

Let $I$ be the point of tangency of $(C_T)$ and $(C_{T'})$.

Question: how can we describe the locus of $I$?

(sketched as the magenta curve on Fig. 2.)

My work: I have obtained through tedious calculations an unexpected linear relationship between parameters $T$ and $T'$ which is:

$$T=(3-2 \sqrt{2})T'\tag{4}$$

Using (4), I have tried to obtain the locus of $I$ as the envelope of chords defined by the line segment joining the centers of circles $C_T,C_{T'}$ using homographies but to no avail.

---

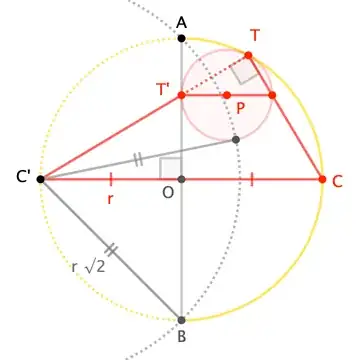
Edit: Nice solution using inversion (a little different from the solution given in a comment by Blue).

'Refer to Fig. 3). Consider inversion with pole $S(0,-1)$ and power $2$ meaning that $M$ is exchanged with $M'$ iff $S,M,M'$ are aligned and $SM.SM'=2$. Its circle of inversion is the black circle (center $S$, radius $\sqrt{2}$). It is easy to see that any circle of family (F) is globally invariant. This is in particular the case for the two blue circles. As the image by inversion of two tangent curves in a certain point $I$ is two tangent curves with contact point $I'$ where $M'$ is the image of $M$, point $I$ is invariant, establishing that $I$ belongs to the circle of inversion.$\square$

As a consequence, tangency points $T_1$ and $U_1$, $T_2$ and $U_2$, are exchanged, meaning that $S,T_1,U_1$ and $S,T_2,U_2$ are aligned.

Fig. 3.

Remark: Two properties of circles of family (F) deserving to be known:

http://www.gogeometry.com/problem/p311_circle_inscribed_semicircle_chord.htm

http://www.gogeometry.com/problem/p310_semicircle_circle_tangent_angle.htm

Answer 1

$$(x_1,y_1)=\left(\frac{T-1}{T+1},\frac{2T}{(T+1)^2}\right)\\ (x_2,y_2)=\left(\frac{U-1}{U+1},\frac{2U}{(U+1)^2}\right)\\ (x_1-x_2)^2+(y_1-y_2)^2=(y_1+y_2)^2\\ \frac{4(T-U)^2}{(T+1)^2(U+1)^2}=4y_1y_2=\frac{16TU}{(T+1)^2(U+1)^2}\\ T^2-6TU+U^2=0$$ The tangent point is $(x,y)=$
$$(y_2(x_1,y_1)+y_1(x_2,y_2))/(y_1+y_2)\\ =\left(\frac{U(T^2-1)+T(U^2-1)}{U(T+1)^2+T(U+1)^2},\frac{4TU}{U(T+1)^2+T(U+1)^2}\right)\\ \frac{4x}y=T-\frac1T+U-\frac1U\\ \frac4y=T+2+\frac1T+U+2+\frac1U\\ \left(\frac4y-4\right)^2=\left(\frac{4x}y\right)^2+4(T+U)(\frac1T+\frac1U)\\ (1-y)^2=x^2+2y^2\\x^2+(y+1)^2=2$$

Answer 2

There's something more fundamental going on here.

---

Consider any circle $\bigcirc P$ tangent to the semicircle $ACB$ at $T$ and the diameter at $T'$. (My figure is rotated.) Let $\overline{CC'}$ be the perpendicular diameter with $C$ the midpoint of the semicircle.

Thales' Theorem guarantees that right angle $\angle CTC'$ subtends parallel diameters of $\bigcirc P$ and $\bigcirc O$; thus, $C'$, $T$, $T'$ are collinear, and $\triangle CTC'\sim\triangle T'OC'$, so that $$|C'T||C'T'|=|C'C||C'O|=2r^2$$ That is, the power of $C'$ with respect to $\bigcirc P$ is independent of $P$. Consequently,

• the tangent segments from $C'$ to any circle is $\sqrt{2r^2}=r\sqrt{2}$; and
• $C'$ lies on the radical axis of any pair of circles.

In the specific case of a pair of inscribed circles that are tangent to each other at a point $I$, the mutual tangent line through $I$ is their radical axis, necessarily meeting $C'$. Moreover, $\overline{C'I}$, being a tangent segment to each circle, has length $r \sqrt{2}$. We conclude that $I$ lies on the circle of radius $r\sqrt{2}$ about $C'$. $\square$

Answer 3

Observe that the point of tangency divides the segment between the centers in the ratio of the radii, that is, in the ratio $y(T')/y(T)$. Therefore, if you call $(U,V)$ the point of tangency, $$ U(T)=x(T)+\frac{y(T')}{y(T)}(x(T')-x(T));\quad V(T)=y(T)+\frac{y(T')}{y(T)}(y(T')-y(T)) $$ where $T'$ is expressed through $T$ using the relation you found (assuming it is correct).

Answer 4

HINT:

Apply a transformation that makes the problem simpler ( more symmetric). Given two circle there exists an inversion that transforms them into two circles of equal radii. Now the problem has a (line of ) symmetry. This can be done in higher dimensions too.

The symmetry line is in fact a circle $C$ such that the reflection in $C$ takes one circle to the other. Note that the reflection with respect to a circle is an intrinsic notion in the circle geometry. However, a circle has no center. Only after we choose the point at infinity, its reflection with respect to the circle will be the "center".