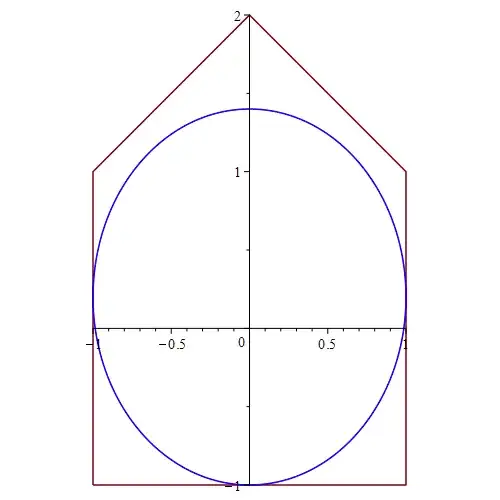
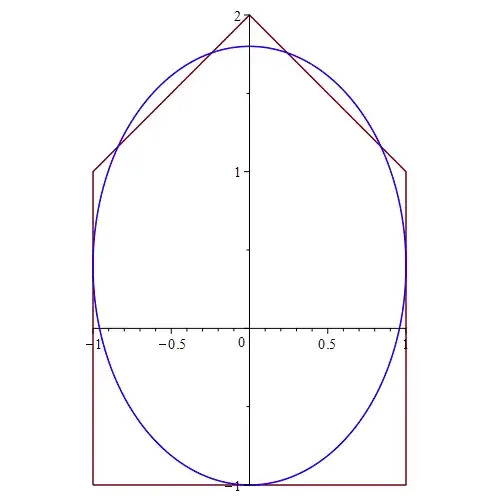
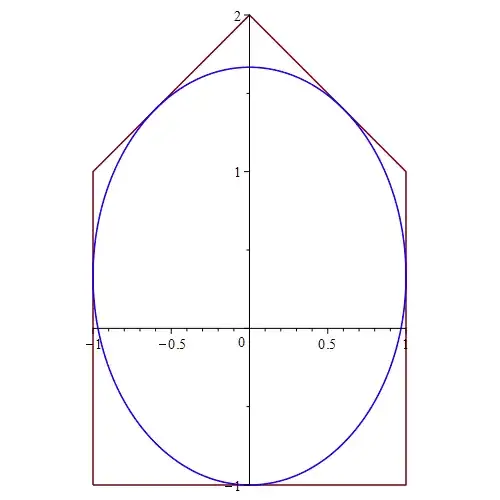
If a polygon is circumscribed to a circle, then the bisectors of its internal angles all meet at a same point. Hence, for part a) just show that this is not the case.
For b) it is a general theorem that there always exists a conic tangent to five given lines. In particular, if the lines form a convex pentagon then the conic is an ellipse.
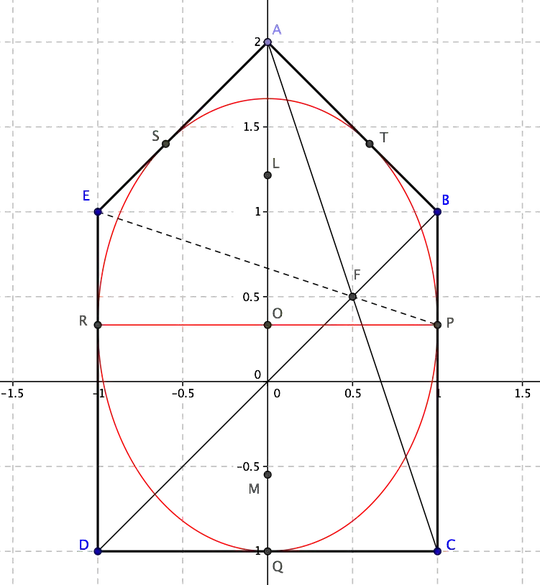
There is a simple geometric construction for the ellipse inscribed in a given convex pentagon $ABCDE$. One can, first of all, find tangency points $PQRST$ (see figure below). Draw, for instance, diagonals $AC$ and $BD$, meeting at $F=(1/2,1/2)$. Line $EF$ meets then side $BC$ at tangency point $P=(1,1/3)$.
This construction depends on Brianchon's theorem:
The three opposite diagonals of every hexagon circumscribing a conic
are concurrent.
In fact, if $P$ is the tangency point on $BC$, we can view $ABPCDE$ as a limiting case of a hexagon circumscribed to the ellipse. Hence diagonals $AC$, $BD$ and $EP$ must intersect at the same point $F$.
For a generic pentagon one would go on finding the other tangency points and remembering then that the line, passing through the intersection point of two tangents to an ellipse and through the midpoint of their tangency points, also passes through the center of the ellipse. Once the center is found one can construct a pair of conjugate diameters and finish then the construction by standard techniques.
In this particular case the construction is simpler, as by symmetry we know that major axis of the ellipse lies on $y$-axis and $PR$, parallel to $x$-axis, is minor axis. Hence semi-minor axis $PO$ has a length $b=1$ and semi-major axis $QO$ has a length $a=4/3$. Focal distance is then $c=\sqrt{a^2-b^2}=\sqrt7/3$ and from that we can find foci $L$ and $M$.