Ellipse in the triangle

Question

Find the equation of an ellipse if its center is S(2,1) and the edges of a triangle PQR are tangent lines to this ellipse. P(0,0), Q(5,0), R(0,4).
My attempt: Let take a point on the line PQ. For example (m,0). Then we have an equation of a tangent line for this point: $(a_{11}m+a_1)x+(a_{12}m+a_2)y+(a_1m+a)=0$, where $a_{11}$ etc are coefficients of our ellipse: $a_{11}x^2+2a_{12}xy+a_{22}y^2+2a_1x+2a_2y+a=0$. Now if PQ: y=0, then $(a_{11}m+a_1)=0$, $a_{12}m+a_2=1$, $a_1m+a=0$.I've tried this method for other 2 lines PR and RQ and I got 11 equations (including equations of a center)! Is there a better solution to this problem?

Answer 1

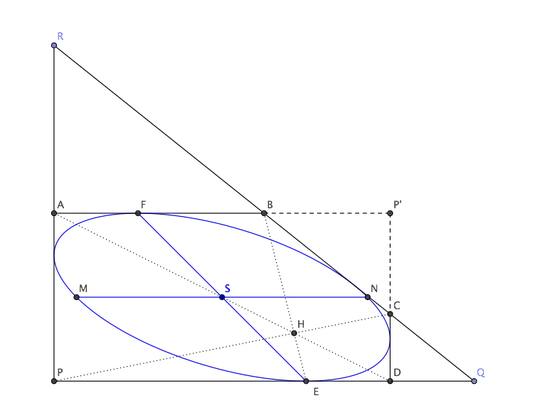
Here's a geometric construction for the ellipse.

Reflect lines $PQ$ and $PR$ about centre $S$ to $AP'$ and $DP'$, which are also tangent to the ellipse. Hence the ellipse is inscribed into pentagon $ABCDP$.

There is a simple construction to find tangency points (see here for a proof): if diagonals $PC$ and $DA$ of the pentagon meet at $H$, line $BH$ intersects $PD$ at tangency point $E=(3,0)$. One can just repeat this construction to find the other four tangency points and plug their coordinates into the generic equation of a conic, to get its coefficients.

Otherwise, reflect $E$ about $S$ to find a diameter $EF$. Conjugate diameter $MN$ is parallel to $PD$ and $MS^2=PS^2-ES^2$ (because $P$ lies on the director circle). Once we have two conjugate diameters we can construct the axes of the ellipse as explained here.

Answer 2

A very different answer, inspired by a property which is well described in pages 139-142 of the book "Mathematical Plums" by G.D. Chakerian, edited by Ross Honsberger, available as a Google book.

Fig. 1: Desmos graphical representation._

The construction we are going to give is based on barycentric coordinates of center $S$:

$$\left(\dfrac{area(SBC)}{area(ABC)},\dfrac{area(ASC)}{area(ABC)},\dfrac{area(ABS)}{area(ABC)}\right)=(0.35, 0.25, 0.40) \approx \underbrace{(7, 5, 8)}_{\text{non normalized}}$$

Let us build a triangle $PRT$ with sides $(7, 5, 8)$ with common side $PR$ with the initial triangle, in order to have simpler computations.

The construction that we are going to do is based on two principles:

• the incenter $I$ of triangle $PRT$ has the same barycentric coordinates as $S$ w.r.t. triangle $PRQ$.

• there exists a linear correspondence mapping triangle $PRT$ onto triangle $PRQ$.

The coordinates of $T$ are

$$(x,y)=(4,4 \sqrt{3}).$$

They are found by solving the following system:

$$\begin{cases}x^2+y^2&=&8^2\\(x-5)^2+y^2&=&7^2\end{cases}$$

Now, consider the following linear transform :

$$A=\begin{pmatrix}1&1\\0&\sqrt{3}\end{pmatrix} \ \ \ \text{with} \ \ \ A^{-1}=\begin{pmatrix}1&-1/\sqrt{3}\\0&1/\sqrt{3}\end{pmatrix}$$

mapping triangle $PRQ$ onto triangle $PRT$.

As linear mappings preserve barycentric coordinates, center $I$ of the incircle of $PRT$ is the image of $S$ (the center point of the ellipse) by $A$, i.e., has coordinates:

$$\begin{pmatrix}1&1\\0&\sqrt{3}\end{pmatrix}\begin{pmatrix}2\\1\end{pmatrix}=\begin{pmatrix}3\\ \sqrt{3}\end{pmatrix}$$

Therefore the incircle has radius $r=\sqrt{3}$ giving it the following parametric equations:

$$\begin{cases}x(t)&=&3+\sqrt{3}\cos(t)\\y(t)&=&\sqrt{3}+\sqrt{3}\cos(t)\end{cases}\tag{1}$$

Coming back to triangle $PRQ$ by applying $A^{-1}$ to (1) ; finally, we obtain the following equations for the ellipse:

$$\begin{cases}X(t)&=&2(1+\cos(t))\\Y(t)&=&1+\frac12(-\cos(t)+\sqrt{3}\sin(t))\end{cases}\tag{2}$$

Important: the following rich article in Forum Geometricum has a cousin approach with many results/remarks, based in particular on what they call the perspector point which is the image by $A^{-1}$ of the Gergonne point of triangle $PRT$.

Remark: $S$ was "a priori" eligible as the center of a certain inscribed ellipse because it is inside the midpoint triangle of triangle $PQR$.

Here is a GeoGebra construction (many thanks to @Toby Mak who made it).

Answer 3

Translate the center to the origin.. the triangle translates to

The translated points become $(-2,-1), (3,-1), (-2,3)$

I considered this on the projective plane, I don't know if that makes it any easier, but that is what I did... if you don't know projective geometry, just set $z = 1$ in everything that follows.

$\begin {bmatrix} x&y&z\end{bmatrix} \begin {bmatrix} A&B&0\\B&C&0\\0&0&D\end{bmatrix} \begin{bmatrix} x\\y\\z\end{bmatrix} = 0$

Describes a cone, which when it intersects the plane $z = 1$ forms the ellipse

i.e. $Ax^2 + 2Bxy + Cy^2 + D = 0$

The planes $x + 2z = 0, y+z = 0$ and $4x + 5y - 7z = 0$ are tangent to the cone.

Consider the triplet $(B,-A, 1)$

$\begin {bmatrix} A&B&0\\B&C&0\\0&0&D\end{bmatrix} \begin{bmatrix} B\\-A\\1\end{bmatrix} = \begin{bmatrix} 0 \\ B^2 - AC \\ D \end{bmatrix}$

If $A = 1$ this point lies in the plane $y + z = 0.$ And if $D = B^2 - AC$

$\begin{bmatrix} B&-1&1\end{bmatrix}\begin{bmatrix} 0 \\ B^2 - AC \\ B^2 - AC \end{bmatrix}= 0$

The point is on our cone.

Similarly $(-\frac {C}{2},\frac {B}{2}, 1)$

$\begin {bmatrix} A&B&0\\B&C&0\\0&0&B^2 - AC\end{bmatrix} \begin{bmatrix} -\frac {C}{2}\\ \frac {B}{2}\\1\end{bmatrix} = \begin{bmatrix} \frac 12 (B^2 - AC) \\ 0\\ B^2 - AC\end{bmatrix}$

If $C = 4$ the point is on the plane $x + 2z = 0$ and on the cone. Our matrix thus far.

$\begin {bmatrix} 1&B&0\\B&4&0\\0&0&B^2-4\end{bmatrix}$

We just need an equation for the 3rd point of tangency.

$(\frac {4C - 5B}{7}, \frac {5A-4B}{7}, 1)$

If it is in the plane $4x + 5y - 7z = 0$

$4\frac {4C - 5B}{7} + 5\frac {5A - 4B}{7} - 7 = 0\\ 4\frac {16 - 5B}{7} + 5\frac {5 - 4B}{7} - 7 = 0\\ 64 - 40 B + 25 - 49 = 0\\ 40-40B = 0\\ B = 1$

And finally we need to check to see if this point is on the cone.

$\begin {bmatrix} 1&1&0\\1&4&0\\0&0&-3\end{bmatrix} \begin{bmatrix} \frac {11}{7}\\ \frac {1}{7}\\1\end{bmatrix} = \begin{bmatrix} \frac {12}7 \\ \frac {15}{7} \\-3\end{bmatrix}$

$\begin{bmatrix} \frac {11}{7} & \frac {1}{7} & 1\end{bmatrix} = \begin{bmatrix} \frac {12}7 \\ \frac {15}{7} \\-3\end{bmatrix} = \frac {132 + 15}{49} - 3 = 0$

$x^2 + 2xy + 4y^2 - 3 =0$

And finally translate back to the original coordinates

$(x-2)^2 + 2(x-2)(y-1) + 4(y-1)^2 - 3 = 0$

Answer 4

The triangle vertices are $P_1 (0,0), Q_1 (5, 0), R_1 (0, 4) $

The equation of the ellipse in matrix-vector form is

$ (r - C)^T Q (r - C) = 1 $

where $C = (2, 1) $ is the center , and $Q$ is a $2 \times 2$ symmetric matrix.

Drawing the triangle, we realize that the required ellipse is tangent to the $x$ axis, the $y$ axis, and the line $y = 5 - \frac{5}{4} x $.

Starting with the $x$ axis, we know that the gradient will be pointing in the $-j$ direction.

Now the gradient $g = 2 Q (r - C) $. If $r_1$ is the tangent point to the ellipse on the $x$ axis then we must have

$ Q(r_1 - C) = \alpha (-j) $

So that $(r_1 - C) = - \alpha Q^{-1} j $

Pluggin this into the ellipse equation gives us $\alpha = \dfrac{1}{\sqrt{ j^T Q^{-1} j }} $

Therefore, $ r_1 - C = - \dfrac{ Q^{-1} j }{\sqrt{ j^T Q^{-1} j } } $

Note that $r_1$ is a point on the $x$ axis, so its $y$ coordinate is zero, i.e. $j^T r_1 = 0 $. Hence

$ j^T (r_1 - C) = - j^T C = - C_y = - \sqrt{ j^T Q^{-1} j } $

Hence, $C_y = 1 = \sqrt{ j^T Q^{-1} j } = Q_{22}^{-1} $

Similar to the above reasoning, we find that $C_x = \sqrt{i^T Q^{-1} i} = Q_{11}^{-1} $

Hence, so far, $Q^{-1} =\begin{bmatrix} 4 && Q_{12}^{-1} \\ Q_{12}^{-1} && 1 \end{bmatrix} $

To find the last unknown, we use the the third condition, which is tangency with the line $y = 5 - \frac{5}{4} x $

The vector $QR = (-5, 4) $ so the unit normal vector to $QR$ is $n = \dfrac{1}{\sqrt{41}} (4, 5) $

Similar to the first tangency analysis with the $x$ axis, we have

$ r_3 - C = \gamma Q^{-1} n $

Plugging this into the ellipse equation results in $\gamma = \dfrac{1}{\sqrt{n^T Q^{-1} n }} $

Therefore, $ n^T (r_3 - C) = n^T (R_1 - C) = n^T (Q_1 - C) = \sqrt{ n^T Q^{-1} n } $

Now $ n^T (R_1 - C) = n^T ( (0,4) - (2, 1) ) = \dfrac{1}{\sqrt{41}} ((4, 5) \cdot (-2, 3) = \dfrac{7}{\sqrt{41}}$

And, $n^T Q^{-1} n = \dfrac{1}{41} ( 4 (4)^2 + 1 (5)^2 + 2 Q_{12}^{-1} (4)(5) )$

Hence $ 40 Q_{12}^{-1} = -40 $ From which $Q_{12}^{-1} = -1 $

Thus, $Q^{-1} = \begin{bmatrix} 4 && -1 \\ -1 && 1 \end{bmatrix} $

Inverting, we get $Q = \dfrac{1}{3} \begin{bmatrix} 1 && 1 \\ 1 && 4 \end{bmatrix} $

Plugging $Q$ in the ellipse equation and expanding gives

$ (x-2)^2 + 2 (x-2)(y-1) + 4 (y-1)^2 = 3 $