Spinning a disk and painting one half - probability whole disk is painted after $n$ steps?

Question

This is a follow-up question based on a conjecture of mine of this question (which phrases the problem slightly differently but functionally identical).

Suppose we randomly spin a disk and then paint its right half, repeatedly. What is the probability $p(n)$ that after $n$ iterations the entire disk is painted?

To disambiguate, let $D$ be a unit-size disk centered on $(0, 0)$. At each step we rotate $D$ clockwise around its center by $\alpha \sim \mathcal{U}(0, 360)$ degrees, and then paint the semicircle where $x \geq 0$. We repeat this (with a new random $\alpha$ every time) until the entire disk is painted. Then $p(n)$ is the probability this process stops after $n$ iterations, and the probability we're interested in.

---

In the previous question it's proven that the expected number of iterations to fully paint the disk is $\sum_{n=1}^\infty p(n)n = 5$.

I conjecture that $p(n) = 2^{-n}(2n - 4)$ for $n \geq 3$ and $0$ otherwise, which perfectly matches my simulated data, and has the right expectation. But I haven't been able to prove it.

So is my conjecture correct and if yes what is a proof?

Answer 1

Let $X_n$ be the nonpainted fraction of the circle after $n$ steps and let $Y_n=1-2X_n$. We have $Y_1=0$ and we easily find that, for $n\ge 1$, $Y_{n+1}=$

• $Y_n$ with probability $Y_n/2$
• $1$ with probability $Y_n/2$
• A uniform random number in $[Y_n,1]$ with probability $1-Y_n$

For $n\ge 2$, let $f_n:(0,1)\to \mathbb{R}_+$ be the probability distribution of $Y_n$ (so that the integral over $(0,1)$ of $f_n$ is the probability that $Y_n\ne 1$). We have $f_2(y)=1$ for all $y$ and our description of $Y_{n+1}$ gives us the recursion: $$f_{n+1}(y)=\frac{y}{2}f_n(y)+\int_0^y f_n(t) dt$$ This recursion is easily solved and we find (for $n\ge 2$) : $f_n(y)=\frac{n(n-1)}{2^n}y^{n-2}$.

Hence the probability that $Y_n=1$ (i.e. that the circle is fully painted after $n$ steps) is $$1-\int_0^1 f_n(y)dy = 1- \int_0^1 \frac{n(n-1)}{2^n}y^{n-2} dy=1-\frac{n}{2^{n-1}}$$

So for the probability that exactly $n$ steps are needed (and not less), it is (for $n\ge 3$) : $$\left(1-\frac{n}{2^{n-1}}\right)-\left(1-\frac{n-1}{2^{n-2}}\right)=\frac{n-2}{2^{n-1}}$$ as you conjectured.

Answer 2

Let us use a discreet version of the problem and then solve it with the limit

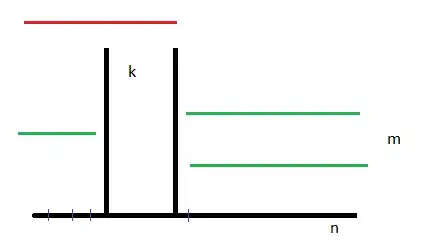
We will count the number of cases when the full coloring happened exactly after $M^{th}$ attempt.

To simplify the reasoning, we will use the equivalent linear version of the problem. We cover a line(circumference of the disk) of length $l$, with lines of length $\frac{l}{2}$. The line is actually a representation of the circle so the end of it is connected to the beginning, meaning a gap, for example, can spill over.

First, we divide a line in $n$ segments.

In the picture, we have $m$ attempts that have created a gap of $k > 0$ segments in length. (On the disk, this would correspond to the uncolored angle $\frac{k2\pi}{n}$.)

In the end, at exactly the $m+1^{th}$ attempt, $m+1=M$, we have managed to color the entire disk. (This is the red-line attempt in the picture.)

In total, we have $n^{m+1}$ possible outcomes.

In order to create a gap of size $k$, we need two attempts, two half lines, that will neighbor the gap to the left and to the right. For this we need two attempts and this has $m(m-1)$ different possible selections out of $m$ attempts.

Next, a half line can fit into the remaining non-colored region in $\frac{n}{2}-k$ ways, and since we have $m-2$ attempts, that means that we have $(\frac{n}{2}-k)^{m-2}$ possible variants.

One more, since we want to cover the gap at the very end by another half line, we can do this in $\frac{n}{2}-k$ ways.

Not to forget, each gap can be positioned in $n$ different location around the circle (line in the picture).

So the total expression of probability of covering the entire line (circumference of the disk) exactly after the $M^{th}$, $M=m+1$, attempt, where we had a gap of size $k$ before the last draw is:

$$\frac{n \cdot m(m-1)(\frac{n}{2}-k)(\frac{n}{2}-k)^{m-2}}{n^{m+1}}$$

For all possible gaps this is:

$$ \sum_{k=1}^{\frac{n}{2}} \frac{m(m-1)(\frac{1}{2}-\frac{k}{n})^{m-1}}{n}$$

and now we let $n$ to tend to infinity

$$ p(m) = \lim_{n \to \infty} \sum_{k=1}^{\frac{n}{2}} \frac{m(m-1)(\frac{1}{2}-\frac{k}{n})^{m-1}}{n}$$

Maybe not trivial, but not impossible either, we reach:

$$ p(m) = \frac{m-1}{2^m} $$

or

$$ p(M) = \frac{M-2}{2^{M-1}} $$

Adding to the flavor, the expected value of the number of strokes before we paint the entire disk is:

$$ E(M) = \sum_{k=1}^{\infty}p(M) = 0+0+ \sum_{k=3}^{\infty}M\frac{M-2}{2^{M-1}} = 5$$