4

Mark precisely one half of the disk by a line that goes through its center.

The angle of the line has a uniform distribution, meaning there is no preferable direction.

You color one half of the disk and keep on with the same coloring scheme.

What is the average number of attempts that you need to color the entire disk?

Paul Bader
  • 43
  • Conjecture: the probability of ending after $k \geq 3$ coloring steps is $p(k) = 2^{-k}(2k - 4)$. – orlp Feb 21 '21 at 23:06

1 Answers1

3

You need to apply color on average five times (so four or five rotations depending on how you count).

Since we randomly rotate every time WLOG we can assume we always color the right half. I also assume we will always rotate before coloring.

We can represent the uncolored slice simply by a proportion $\alpha$ of the full circle. Let $f(\alpha)$ be the expected number of rotations needed for remaining slice $0 < \alpha \leq \frac{1}{2}$ (the first time around we always color exactly half).

We find that the chance this slice is completely on the right half is $\frac{1}{2} - \alpha$ (consider how much we can rotate $\alpha$ starting from being aligned vertically on one edge to being aligned vertically again on the other edge). In that case we are done.

We get a similar chance for 'completely on the left half', in which case we made no progress.

In the remaining case we get a partial hit (which has chance $1 - 2\cdot(\frac{1}{2} - \alpha) = 2\alpha$), we can take the mean over all possible proportions that are left (which have uniform equal chance of appearing by rotational symmetry):

\begin{align} f(\alpha) &= 1 +\left(\frac{1}{2} - \alpha\right) \cdot f(\alpha) + 2\alpha\cdot\lim_{\epsilon \to 0} \frac{1}{\alpha - \epsilon}\left[\int_\epsilon^\alpha f(p)\mathrm{d}p\right] \end{align} $$\left(1 + 2\alpha\right)f(\alpha) - 2 = 4\alpha\cdot\lim_{\epsilon \to 0}\frac{1}{\alpha - \epsilon} \left[\int_\epsilon^\alpha f(p)\mathrm{d}p\right]$$

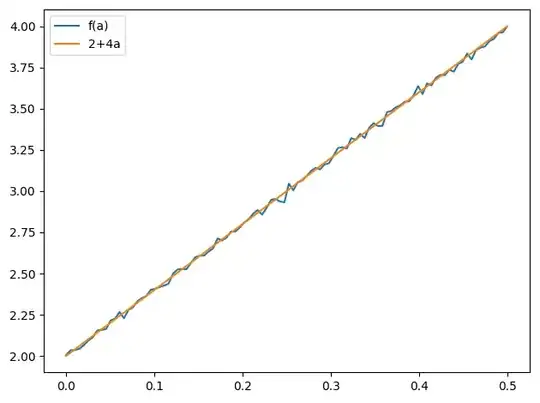
Now as an ansatz*, let $f(\alpha) = 2 + 4\alpha$. Then:

\begin{align} \left(1 + 2\alpha\right)(2 + 4\alpha) - 2 &= 4\alpha\cdot \lim_{\epsilon \to 0}\frac{1}{\alpha - \epsilon} \left[\int_\epsilon^\alpha (2 + 4p)\mathrm{d}p\right]\\ 8\alpha +8\alpha^2 &= 4\alpha\cdot \lim_{\epsilon \to 0}\frac{2\alpha + 2\alpha^2 - 2\epsilon - 2\epsilon^2}{\alpha - \epsilon}\\ 8\alpha +8\alpha^2 &= 4\alpha \cdot (2 + 2 \alpha)\quad \checkmark \end{align}

Thus our final answer is $1 + f\left(\frac{1}{2}\right) = 5$.

My ansatz was generated programmatically:

import numpy as np
import matplotlib.pyplot as plt

def f(a):
    r = np.random.rand()
    if r < 2a:
        # Partial hit.
        return 1 + f(np.random.rand()  a)
    if r - 2*a < 0.5 - a:
        # Complete miss.
        return 1 + f(a)


# Complete hit.
return 1




def favg(a, it=10000):
    return sum(f(a) for _ in range(it))/it


A = np.linspace(0.0001, 0.5, 100)
fa = np.array([favg(a) for a in A])
plt.plot(A, fa, label="f(a)")
plt.plot(A, 2+4*A, label="2+4a")
plt.legend()
plt.tight_layout()
plt.show()

graph

orlp
  • 10,508
  • The limit is unnecessary, we have an integral equation $(1+2a)f(a) = 2 + 4 \int_0^a f(b)\mathrm{d}b$ with an obvious boundary condition f(0) = 2 (put a=0), differentiating, we get a differential eq. (1+2a)f'=2f, which has a solution f = K(1+2a), with the boundary condition applied, we get f = 2(1+2a) – Machinato Feb 21 '21 at 21:23
  • @Machinato I'm not too familiar with differential equations, and I know that in the end the limit didn't end up mattering, but I wanted to include it just for rigor's sake. I'm sure that a seasoned mathematician will end up swooping along, posting a 5 line proof, I just posted how I solved it :) – orlp Feb 21 '21 at 21:25
  • your answer overwhelmed me, I have seen usages of the mean recurrence many times before as it is a „common” but powerful trick for ex. random walk termination or in the Markov processes. What is very novel to me is the continuous part, I would like to see more problems using this. – Machinato Feb 21 '21 at 23:54