Emphasis added: I'm trying to find a real world interpretation of division algorithm
Division in $\mathbb{Z}$ has a well defined analogue in our physical world. Since, in general, division algorithm $a=bq+r$ is not unique, does it have an easy-to-understand meaning? Let's say $a,b,q,r \in \mathbb{Z}[\sqrt{11}]$, $b \ne 0$. Suppose $a=1$ and $b=2$, we have,
\begin{align} 1 + \sqrt{11} &= (6-2\sqrt{11})\ (-3-\sqrt{11}) + (-3+\sqrt{11}) \\ &= (6-2\sqrt{11})\ (-4-\sqrt{11}) + ( 3-\sqrt{11}) \\ &= (6-2\sqrt{11})\ (-103-31\sqrt{11}) + ( -63- 19\sqrt{11}) \\ &= (6-2\sqrt{11})\ ( 96-31\sqrt{11}) + (-1257+379\sqrt{11}) \\ &= \dots \text{and many more, although I don't know if it is finite or not.} \end{align}
And note that: \begin{align} N(\alpha) = N(1 + \sqrt{11}) = 10 &\text{ and } N(\beta) = N(6-2\sqrt{11}) = 8 \\ N(q_{1}) = N(-3-\sqrt{11}) = 2 &\text{ and } N(r_{1}) = N(-3+\sqrt{11}) = 2 \\ N(q_{2}) = N(-4-\sqrt{11}) = 5 &\text{ and } N(r_{2}) = N(3-\sqrt{11}) = 2 \\ N(q_{3}) = N(-103-31\sqrt{11}) = 38 &\text{ and } N(r_{3}) = N(-63- 19\sqrt{11}) = 2 \\ N(q_{4}) = N(96-31\sqrt{11}) = 1355 &\text{ and } N(r_{4}) = N(-1257+379\sqrt{11}) = 2. \\ \end{align}
Background added: I do aware of the follows
A norm is well-defined if $N(\alpha\beta) \ge N(\alpha)$. Note that $N(\alpha\beta) = N(\alpha)N(\beta)$ and $N(\alpha)=1 \iff \alpha\ \text{is a unit}$.
There is no doubt that $\mathbb{Z}[\sqrt{11}]$ is norm-euclidean. With $a,b \in \mathbb{Z}[\sqrt{11}]$, $b \ne 0$, suppose the nearest lattice point to $a/b \in \mathbb{Q}[\sqrt{11}]$ is $m+n\sqrt{11} \in \mathbb{Z}[\sqrt{11}]$, one possible division algorithm can be defined by considering six lattice points as quotient $q=(m+x)+(n+y)\sqrt{11}$ with $(x,y) \in \{ (0,0),\ (1,0),\ (-1,0), (2,0),\ (2,1),\ (-5,2) \}$, which satisfies $N(r)<N(b)$ if $r \ne 0$.
I pick $\mathbb{Z}[\sqrt{11}]$, since it is the first quadratic integer ring, among $\mathbb{Z}[\sqrt{d}]$ with $d \in \{ -2, -1,\ 2,\ 3,\ 6,\ 7,\ 11,\ 14,\ 19 \} $, that it is not trivial to prove it is a Euclidean domain. Although $\mathbb{Z}[\sqrt{14}]$ is Euclidean but it is not norm-Euclidean.
Let me rephrase my question (19th February)
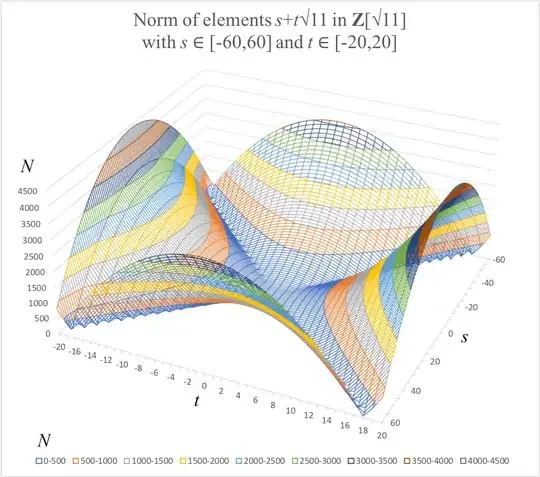
Perhaps a more fundamental question is that do different definitions of norm have geometric meaning. Let $R=\mathbb{Z}[\sqrt{d}] = \{ s+t\sqrt{d} : s,t \in \mathbb{Z} \}$ be a quadratic integer ring. The most usual definition of norm is $N: R \setminus \{ 0 \} \rightarrow \mathbb{Z}_{\ge 0}$ by setting $s+t\sqrt{d} \mapsto |s^2 - dt^2 |$. For negative values of $d$, $N$ is the modulus squared for any given element in $R$. For $d=-1$ and $d=-2$, elements in $\mathbb{Z}[i]$ and $\mathbb{Z}[\sqrt{-2}]$ are nicely ordered (along $\mathbb{Z}_{\ge 0}$) in concentric circles and ellipses respectively by their moduli squared. For positive values of $d$, an element (not $R$) has a division algorithm, if $\alpha/\beta$ falls within a starfish shape, enclosed by two pairs of hyperbolae, with a good choice of quotient $q$. Elements of the same (or close enough by magnitude) norms are no longer nicely ordered (geometrically) but all over the places.
Thanks @BillDubuque for the Lenstra papers. They are very useful to a non maths person like me.