I am a novice and learning to write simple proofs. I welcome corrections and suggestions. Below is a detailed workout. Most maths students will find it unnecessarily verbose. Oppenheim (1934) proved, among other proofs, that $\mathbb{Z}[\sqrt{11}]$ has a division algorithm and hence a Euclidean domain. We unpack his proof here.
Let $R = \mathbb{Z}[\sqrt{11}] = \{ s+t\sqrt{11} : s,t \in \mathbb{Z} \} $ be a quadratic integer ring. It is said to be a Euclidean domain if there are:
(a) a well defined norm $N(\alpha) \leq N(\alpha\beta)$, and
(b) a division algorithm $\alpha = q \beta +r$ such that either (i) $r=0$, or (ii) $r \ne 0$ and $N(r) < N(\beta)$
with $\alpha,\beta \in R$, $\beta \ne 0$ and some quotient and remainder $q,r \in R$.
Let $\alpha = s+t\sqrt{11} \in R$. Define norm $N: R \setminus\{0\} \rightarrow \mathbb{Z}_{\geq 0}$ by setting $\alpha \mapsto |s^2-11t^2|$, which is well defined in $R$. Proof omitted. Norm $N$ is also well defined in $\mathbb{Q}[\sqrt{11}]$. Proof omitted. There exists $\alpha/\beta \in \mathbb{Q}[\sqrt{11}] = \{ s+t\sqrt{11} : s,t \in \mathbb{Q} \} \supset R $ with a numerator and a denominator $\alpha, \beta \in R$. Proof omitted.
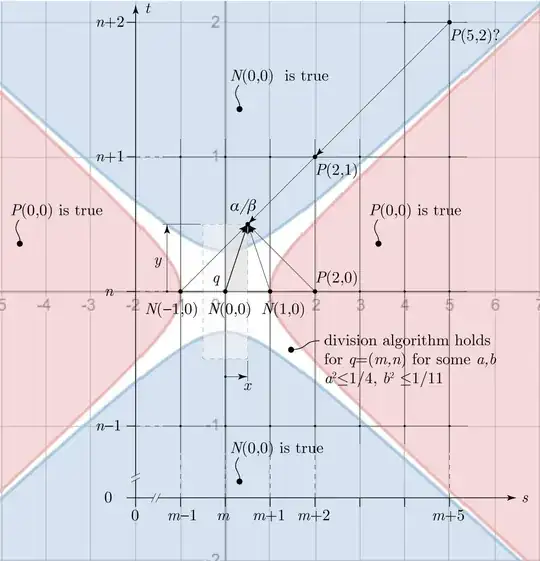
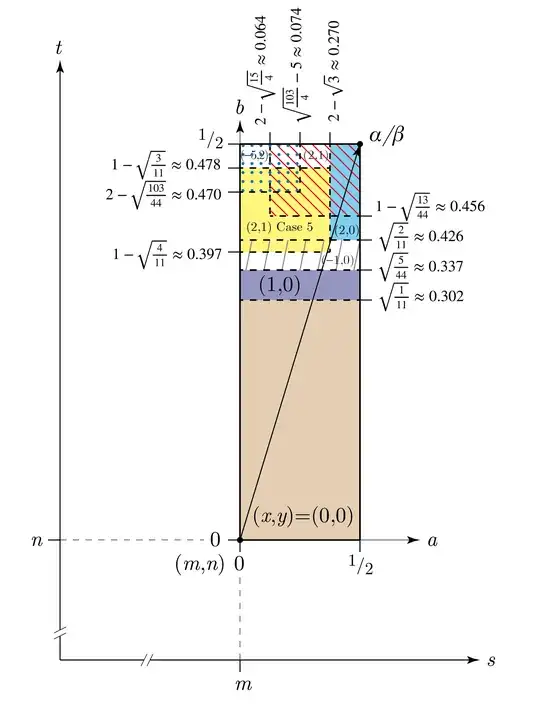
Suppose the nearest lattice point to point $\alpha / \beta$ is $m+n\sqrt{11} \in R$ (i.e. $m,n \in \mathbb{Z}$) with $\alpha / \beta = (m+n\sqrt{11}) + (a+b\sqrt{11})$, $a,b \in \mathbb{Q}$, $-\frac{1}{2} \leq a \leq \frac{1}{2}$ and $-\frac{1}{2} \leq b \leq \frac{1}{2}$. We will consider lattice point $(m,n) = m+n\sqrt{11}$ and five others nearby. They, $(m+x,n+y)$ with $(x,y) \in \{ (0,0), (1,0), (-1,0), (2,0), (2,1), (5,2) \} $, are candidate quotients to a division algorithm. By considering only positive values of $a,b$ such that $0 \leq a \leq \frac{1}{2}$ and $0 \leq b \leq \frac{1}{2}$, similar arguments could be made for the three other quadrants by symmetry. With $q=(m+x,n+y)$, rewrite $\alpha = q \beta +r$ as:
\begin{align}
\alpha / \beta &= q + r/\beta \\
&= q + \big( (a+b\sqrt{11}) - (x+y\sqrt{11}) \big)
\end{align}
Condition (b)(ii) if $r \ne 0$, $N(r) < N(\beta)$ is true $\iff$ $N(r)/N(\beta) < 1$ $\iff$ $N(r/\beta) < 1$ $\iff$ $N \big( (a+b\sqrt{11}) - (x+y\sqrt{11}) \big)$ $= |(x-a)^2 - 11(y-b)^2| < 1$. Proof omitted.
Proposition: A division algorithm holds for $\mathbb{Z}[\sqrt{11}]$ if both inequalities:
\begin{align}
U(x,y): &\ (x-a)^2 - 11(y-b)^2 < 1 \ \text{and} \\
V(x,y): &\ 11(y-b)^2 - (x-a)^2 < 1 \ \text{are true,}
\end{align}
for all $a,b \in \mathbb{Q}$, $0 \leq a \leq \frac{1}{2}$ and $0 \leq b \leq \frac{1}{2}$, and some $x,y \in \mathbb{Z}$.
Rewrite not $U(x,y)$ and not $V(x,y)$ as $P(x,y)$ and $N(x,y)$ respectively.
\begin{align}
P(x,y): &\ (x-a)^2 \geq 1 + 11(y-b)^2 \\
N(x,y): &\ 11(y-b)^2 \geq 1 + (x-a)^2
\end{align}
Suppose to the contrary that the contrapositive of the above proposition is true. It asserts that a division algorithm does not hold for $\mathbb{Z}[\sqrt{11}]$. Then either $P(x,y)$ or $N(x,y)$ is true for some $a,b$ and all $x,y$.
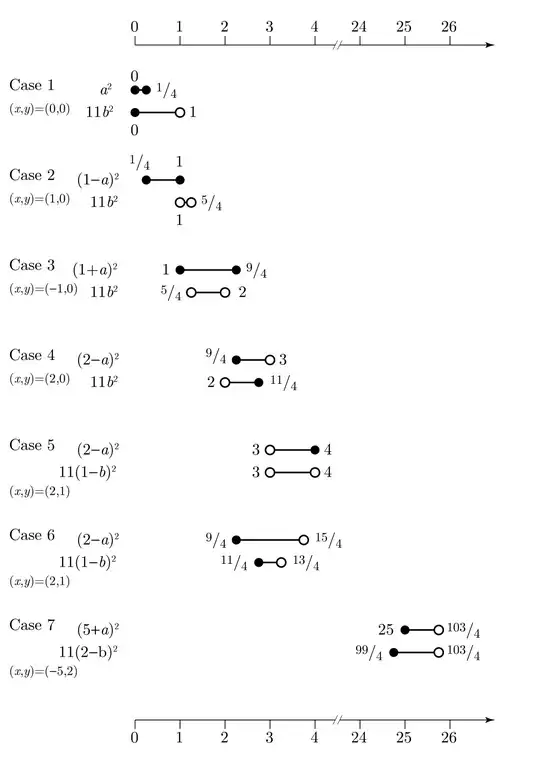
Consider $\mathbf{P(0,0)} : (-a)^2 \geq 1 + 11(-b)^2$. It implies $a^2 \geq 1$. Take the positive root and we have $a \geq 1$ which contradicts $0 \leq a \leq \frac{1}{2}$. Since $P(0,0)$ is false, $N(0,0)$ must hold.
$N(0,0): 11b^2 \geq 1+a^2$
Consider $\mathbf{P(1,0)} : (1-a)^2 \geq 1 + 11b^2$. By $N(0,0)$,
\begin{align}
(1-a)^2 &\geq 1 + 11b^2 \geq 2+a^2 \\
(1-a)^2 &\geq 2+a^2 \\
1-2a+a^2 &\geq 2+a^2 \\
-2a &\geq 1 \\
a &\leq -\frac{1}{2}
\end{align}
which contradicts $0 \leq a \leq \frac{1}{2}$. Since $P(1,0)$ is false, $N(1,0)$ must hold.
$N(1,0): 11b^2 \geq 1 + (1-a)^2$
 https://www.desmos.com/calculator/rhrza9vqpx
https://www.desmos.com/calculator/pccntyashy
https://www.desmos.com/calculator/rhrza9vqpx
https://www.desmos.com/calculator/pccntyashy
Consider $\mathbf{P(-1,0)} : (-1-a)^2 \geq 1 + 11b^2$. By $N(1,0)$,
\begin{align}
(1+a)^2 &\geq 1 + 11b^2 \\
(1+a)^2 - 1 &\geq 11b^2 \geq 1 + (1-a)^2 \\
1 + 2a + a^2 - 1 &\geq 1 + 1 - 2a + a^2 \\
4a &\geq 2 \\
a &\geq \frac{1}{2} \\
\end{align}
Then $a = \frac{1}{2}$ since $0 \leq a \leq \frac{1}{2}$. It follows that:
\begin{align}
(1+\frac{1}{2})^2 - 1 &\geq 11b^2 \geq 1 + (1-\frac{1}{2})^2 \\
\frac{5}{4} &\geq 11b^2 \geq \frac{5}{4}
\end{align}
But $b = \sqrt{ \frac{5}{44} } \notin \mathbb{Q}$ contradicts $b \in \mathbb{Q}$. Since $P(-1,0)$ is false, $N(-1,0)$ must hold.
$N(-1,0): 11b^2 \geq 1 + (1+a)^2$
Consider $\mathbf{N(2,0)} : 11b^2 \geq 1 + (2-a)^2$.
\begin{align}
11b^2 &\geq 1 + (2-a)^2 \geq \frac{13}{4} > \frac{11}{4} \\
b^2 &> \frac{1}{4}
\end{align}
Take the positive root and we have $b > \frac{1}{2}$. But it contradicts $0 \leq b \leq \frac{1}{2}$. Since $N(2,0)$ is false, $P(2,0)$ must hold.
$P(2,0): (2-a)^2 \geq 1 + 11b^2$
Consider $\mathbf{N(2,1)} : 11(1-b)^2 \geq (2-a)^2$. By $N(2,0)$,
\begin{align}
11(1-b)^2 &\geq 1 + (2-a)^2 \geq 1 + 11b^2 \\
11 - 22b + 11b^2 &\geq 1 + 11b^2 \\
9 &\geq 22b \\
b &\leq \frac{9}{22}
\end{align}
By $N(-1,0)$,
\begin{align}
11b^2 &\geq 1 + (1+a)^2 \geq 2 > \frac{81}{44} \\
$b^2 &> (\frac{9}{22})^2
\end{align}
Take the positive root and we have $b > \frac{9}{22}$. But it contradicts $b \leq \frac{9}{22}$. Since $N(2,1)$ is false, $P(2,1)$ must hold.
$P(2,1): (2-a)^2 \geq 1 + 11(1-b)^2$
By $P(2,1)$ and $N(-1,0)$, they imply:
\begin{align}
(2-a)^2 &\geq 1 + 11(1-b)^2 \\
(2-a)^2 &\geq 1 + 11 -22b + 11b^2 \\
(2-a)^2 -12 + 22b &\geq 11b^2 \geq 1 + (1+a)^2 \\
4 -4a + a^2 -12 + 22b &\geq 2 + 2a + a^2 \\
22b &\geq 10 + 6a \\
11b &\geq 5 + 3a
\end{align}
Out of interest. Take the least possible value to the RHS; it implies $11b \geq 5$. Likewise, take the greatest possible value to the LHS; it implies $11 \geq 10 + 6a$ $\implies$ $1 \geq 6a$.
Consider $\mathbf{N(5,2)}: 11(2-b)^2 \geq 1 + (5-a)^2$. By $P(2,1)$, it implies:
\begin{align}
11(2-b)^2 &\geq 1 + (5-a)^2 \\
11(2-b)^2 &\geq 26 -10a +a^2 \\
11(2-b)^2 &\geq (4 - 4a + a^2) + 22 -6a \\
11(2-b)^2 - 22 + 6a &\geq (2-a)^2 \geq 1 + 11(1-b)^2 \\
22 - 44b + 11b^2 + 6a &\geq (2-a)^2 \geq 12 -22b + 11b^2 \\
10 + 6a &\geq 22b \\
5 + 3a &\geq 11b
\end{align}
By $11b \geq 5 + 3a$ and $5 + 3a \geq 11b$, we have $5 + 3a = 11b$. Retrace backwards the argument leading to $5 + 3a \geq 11b$. We have $11(2-b)^2 - 22 + 6a = (2-a)^2 = 1 + 11(1-b)^2$. Take the middle and the RHS of this chain of equality and name it $P'(2,1)$. Establishing the following two equalities are not strictly necessary for this proof. Since Oppenheim (1934) mentioned them, we will include them here. Take the LHS and the middle of the above chain of equality, we have $11(2-b)^2 - 22 + 6a = (2-a)^2$ $\implies$ $11(2-b)^2 = (4 - 4a + a^2) + 22 -6a$ $\implies$ $11(2-b)^2 = 26 -10a +a^2$ $\implies$ $11(2-b)^2 = 1 + (5-a)^2$. Name it $N'(5,2)$. Retrace backwards the argument leading to $11b \geq 5 + 3a$. We have $(2-a)^2 -12 + 22b = 11b^2 = 1 + (1+a)^2$. Take the middle and the RHS of this chain of equality and name it $N'(-1,0)$. And we have:
\begin{align}
P'(2,1)&: (2-a)^2 = 1 + 11(1-b)^2 \\
N'(5,2)&: 11(2-b)^2 = 1 + (5-a)^2 \\
N'(-1,0)&: 11b^2 = 1 + (1+a)^2
\end{align}
By $N'(-1,0)$ and $5 + 3a = 11b$,
\begin{align}
11b^2 &= 1 + (1+a)^2 \\
(11b)^2 &= 11 + 11(1+a)^2 \\
(5+3a)^2 &= 11 + 11(1+a)^2 \\
25 + 30a + 9a^2 &= 22 + 22a + 11a^2 \\
2a^2 - 8a &= 3 > 0
\end{align}
It implies $a<0$ or $a > 4 > \frac{1}{2}$ but they contradict $0 \leq a \leq \frac{1}{2}$. And hence $N(5,2)$ is false, $P(5,2)$ must be true.
$P(5,2): (5-a)^2 \geq 1 + 11(2-b)^2$
Consider $\mathbf{P(5,2)}$, by $N'(-1,0)$, it implies:
\begin{align}
(5-a)^2 &\geq 1 + 11(2-b)^2 \\
25 - 10a + a^2 &\geq 1 + 11(2-b)^2 \\
23 - 12a + 1 + (1 + 2a + a^2) &\geq 1 + 11(2-b)^2 \\
23 - 12a + \big( 1 + (1 + a)^2 \big) &\geq 1 + 11(2-b)^2 \\
23 - 12a + 11b^2 &\geq 45 - 44b + 11b^2 \\
44b &\geq 22 +12a \\
22b &\geq 11 + 6a
\end{align}
Possible range of the LHS is $[0,11]$ and that of RHS is $[11,14]$. Therefore, they only possible values are $b = \frac{1}{2}$ and $a=0$. Substitute $b = \frac{1}{2}$ back into $P(5,2)$, and it asserts,
$(5-a)^2 \geq 1 + 11(2- \frac{1}{2} )^2 = \frac{103}{4} > (\frac{10}{2})^2 = 5^2$
Take the positive root (since negative root $a-5 \geq 0$ is false) and we have $5-a > 5$ $\implies$ $a < 0$. But it contradicts $a = 0$. And hence $P(5,2)$ is false.
Since both $N(5,2)$ and $P(5,2)$ are false, they contradicts the proposition that either $P(x,y)$ or $N(x,y)$ is true for some $a,b$ and all $x,y$. And hence, the proposition that a division algorithm does not hold is false. Therefore, $\mathbb{Z}[\sqrt{11}]$ has a division algorithm and hence a Euclidean domain. $\ \ \ \ \blacksquare$

![Z[sqrt(11)] with max a,b ranges](../../images/31879b67992728fc333afa92c32c80bd.webp)
![Z[sqrt(11)] with max a,b ranges (cases 1,5,6)](../../images/d6644363baa1d6d59b0e9973284c7406.webp)
![Z[sqrt(11)] with max a,b ranges (cases 2,4)](../../images/37e197939798ca8133f021e4b099c958.webp)
![Z[sqrt(11)] with max a,b ranges (case 3)](../../images/b2901e203ce3833fb01a84f6981c407c.webp)
![Z[sqrt(11)] with max a,b ranges (case 7)](../../images/4210901ad3b2123d361892357ac7ef27.webp)
![Z[sqrt(11)] with max a,b ranges (only alg. only)](../../images/c3d11cc5cdbab6d1533d56779b10646a.webp)