This question is inspired by CNC toolpath generation, although I've become interested in it from a more theoretical perspective as well; the practical answer may be to find a CAD software tool that does exactly what I'm asking, but I am more curious about the underlying math and/or algorithms.
To be specific, the relevant real-world problem is to generate an approximation to a polygonal shape with "arbitrarily complex detail", where the approximation represents a curve (splines, conic sections, clothoids, whatever) with the property that its curvature never exceeds a set limit. I'm not sure what exactly "optimal approximation" might mean here, so I'm not going to include that as part of the question, although that is the motivation.
I'm curious about how to define a sort of "continuous, two-sided fillet" smoothing operation on an arbitrary shape like this.
Topics I have looked into:
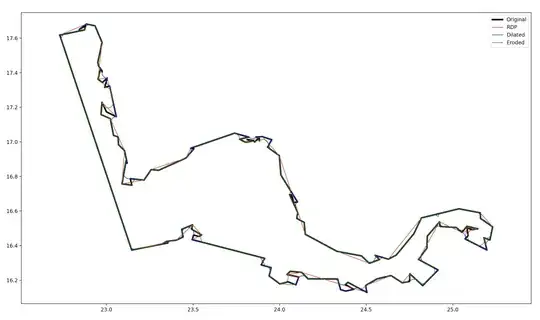
- Ramer-Douglas-Peucker is a basic polygon simplification algorithm, which is useful in cartographic generalization - clearly relevant, but it's not helpful for the curvature aspect.
- Pythagorean-Hodograph curves - curves designed specifically to have easy-to-manipulate representations of arc length, convenient for generating offset curves. I think the curvature should be similarly convenient to work with, but this makes sense for a smooth curve, not for creating a smooth curve from a jagged polygon.
- Minkowski operations - dilation and erosion directly implement interior and exterior filleting. This limits the curvature at every point on the resulting curve, except for cusps.
- Epicycle drawing - This could conceivably be adjusted to only use circles above the size limit, which would result in a curve that generally respects the desired curvature limit. However, the sum of the epicycle components allows for regions of tighter curvature, and even cusps.
None of these seem quite right. I'm wondering if there is some other concept more directly useful here that I'm missing.
Here is an example polygon, which is a segment of a world map border. RDP, erosion and dilation are included as well, showing some of the problems with these approaches:
Note that related questions have been asked here before:
However, I am asking specifically about the problem of simplifying a detailed, jagged polygon. I realize this question may not be totally well-defined, and that's OK. I am interested in any information related to addressing this problem or similar ones.