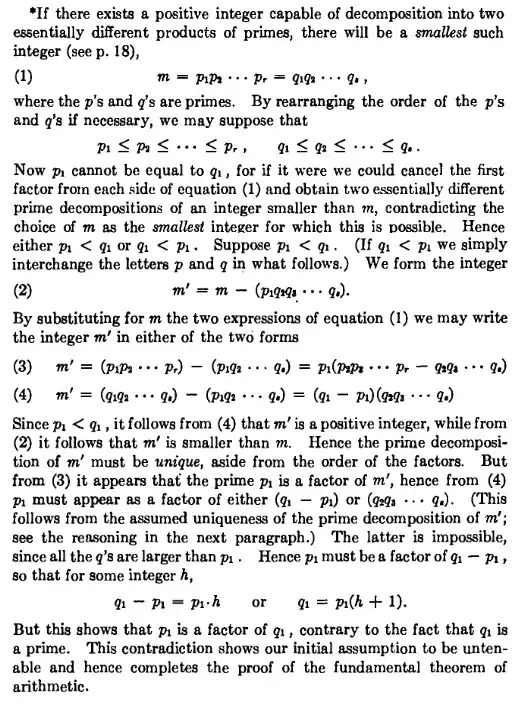Mathematical Induction prime help

Question

I recently obtained "What is Mathematics?" by Richard Courant and I am having trouble understanding what is happening with the Prime Number Unique Factor Composition Proof (found on Page 23).

The first part:

I have looked over it many times but I just don't understand what he is doing and why, as an example, if you remove the first factor from either side of the equation you end up with two essentially different compositions that make up a new smaller integer.

I'm sure it is a simple error on my behalf but I have been stuck on this for a long time so I would appreciate a walkthrough explained clearly or some pointers in the right direction. Thank you.

Answer 1

You want to show that every positive integer can be expressed as a product of prime numbers, secondly you want that such a decomposition is unique (except for the order of factors). Call $\mathscr{F}$ the set of positive integers not satisfying your claim, i.e. the set of positive integers that can be written in more than a single way as a prime product. In terms of $\mathscr{F}$, your claim becomes: show that $\mathscr{F}$ is empty. By contradiction, suppose $\mathscr{F}$ non-empty and look for an absurd.Every non-empty set of positive integers has a smallest element, call $m$ the smallest element of $\mathscr{F}$. Using the book notation, suppose $p_1=q_1$ and cancel the two factors from both sides. Since the two factorizations were supposed to be different, they remain different after that cancellation, producing an element of $\mathscr{F}$, but smallest than $m$, contradicting the definition of $m$ as the smallest element of $\mathscr{F}$. Then $p_1$ is strictly less than $q_1$ or viceversa...

Answer 2

We reframe the logic of the argument, using a variant of induction called Fermat's Method of Infinite Descent.

Call a positive integer bad if it has (apart from order) more than one factorization as a product of prime powers. Note that $1$ is not bad.

We want to show that there are no bad positive integers. Suppose to the contrary that there is a bad positive integer $n_1$.

By the argument in the book, there is then a bad positive integer $n_2\lt n_1$.

By the argument in the book, there is then a bad positive integer $n_3\lt n_2$.

And so on. So if there is a bad positive integer, there is an infinite descending sequence $$n_1\gt n_2\gt n_3\gt n_4\gt \cdots$$ of (bad) positive integers.

However, there is no infinite descending sequence of positive integers!

Instead of using the language of descent. the proof quoted above used the fact that if there is a bad positive integer, there is a smallest bad. The two proofs are completely equivalent, they are really the same proof. However, descent feels more concrete to me.

Remark: The proof that is used in What is Mathematics is a clever one, in that it avoids using "Euclid's Lemma." This lemma essentially says that if a prime $p$ divides $ab$, then $p$ divides $a$ or $p$ divides $b$. The standard proof of the Fundamental Theorem uses Euclid's Lemma. Thus in a sense the proof you quoted uses less machinery than the standard proof, it is, sort of, more "elementary." It pays for that by being quite a bit more complicated, and harder to understand. It is the sort of proof that might be appreciated for its cleverness if one is already familiar with the standard proof.

Answer 3

It appears that the troublesome aspect of the proof is the negative contradictory form of induction that is employed, i.e. the contrapositive of complete induction (Fermat's infinite descent). This is easily eliminated by rewriting the proof to use complete induction, as is done below.

Suppose as inductive hypothesis that the prime factorization of every natural $< m\,$ is unique up to order. We prove that the same holds true for $\,m.\,$ Consider any two prime factorizations of $\,m$

$$\tag{1} m\, =\, p_1 p_2\cdots p_r =\, q_1 q_2\cdots q_s$$

where the $p$'s and $q$'s are primes. By reordering if need be, we may assume that

$$ p_1 \le p_2 \le \cdots \le p_r,\quad q_1 \le q_2 \le \cdots \le q_s$$

We prove $\,\color{#0a0}{p_1 = \ q_1}.\,$ We may assume $\,p_1 \le q_1$ (else change notation: swap $p$ and $q).\,$ Let $$\tag{2} m' = m - p_1 q_2 q_3\cdots q_s$$

By substituting for $\,m\,$ its two factorizations in equation $(1)$ we obtain $$\begin{eqnarray} \tag{3} m' &=\,& p_1 p_2\cdots p_r -\, p_1 q_2\cdots q_s &=\,& p_1 (p_2\cdots p_r -\, q_2 q_3 \cdots q_s) \\ \tag{4} m' &=\,& q_1 q_2\cdots q_s -\, p_1 q_2\cdots q_s &=\,& (q_1-p_1)(q_2 q_3\cdots q_s) \end{eqnarray}$$

Suppose $\,\color{#c00}{p_1 \ne q_1}\,$ Then $\,p_1 < q_1\,$ so it follows by $(4)$ that $\,m'>0$, while $\,m'<m\,$ by $(2).\,$ So, by induction, the prime factorization of $\,m'\,$ is unique, up to order. From $(3)$ it follows that $\,p_1\,$ is a factor of $\, m'.\,$ Thus, by uniqueness, $\,p_1\,$ must also appear as a factor in $(4)$, i.e. as a factor of either $\,q_1 - p_1$ or $\,q_2\cdots q_s.\,$ The latter is impossible, since all the $\,q_i\,$ are primes larger than $\,p_1.\,$ Hence $\,p_1\,$ is a factor of $\,q_1 - p_1,\,$ i.e. there is an integer $\,k\,$ such that $\, q_1 - p_1 = k p_1,\,$ so $\,q_1 = (k\!+\!1) p_1.\,$ Thus $\,p_1\,$ is a factor of $\,q_1,\: $ contra prime $\:q_1 > p_1.\, $ This contradiction proves that our assumption $\,\color{#c00}{p_1\ne q_1}\,$ is false, so $\,\color{#0a0}{p_1 = q_1}\,$ as claimed.

Cancelling $\,\color{#0a0}{p_1\! = q_1}\,$ from both sides of equation $(1)$ and applying the inductive hypothesis, we infer that the smaller number $\, m/p_1 = p_2\cdots p_r =\, q_2\cdots q_s\,$ has unique factorization, so $\, r = s\,$ and $\, p_2\! = q_2,\ p_3\! = q_3,\ldots, p_s\! = q_s.\,$ Hence the factorizations in $(1)$ are the same up to order. $ $ QED

Answer 4

Take a look this is a proof by contradiction you're suposing that the two factorizations are different and getting an absurd (in this case that one prime is divisible by another prime), thus the asumption the factorizations were different is false. m is the smallest choice because you're using the principle of well ordering defined on page 18.. "Every non empty set of positive integers has a smallest member" https://en.wikipedia.org/wiki/Well-order this smallest member is the smallest number you're suposing you can factorize into two different prime factors