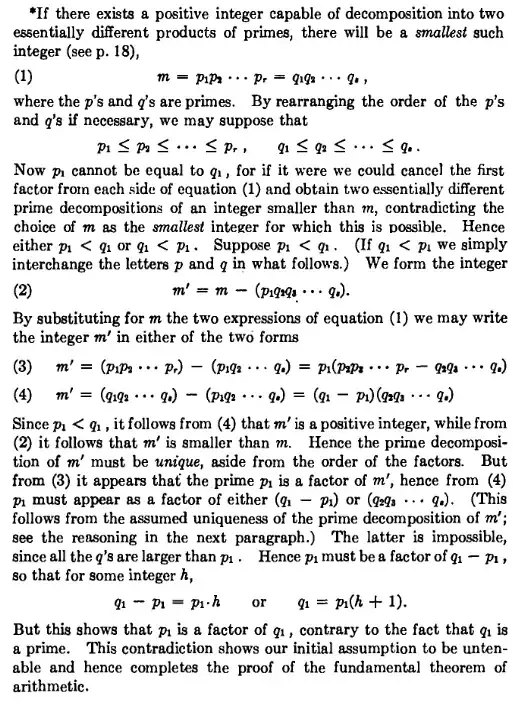2

My previous questions have been on a very similar topics but I am having trouble with understanding this:

enter image description here

I understand that $p_1$ or $q_1$ must be greater than the other but I have no idea what is happening when he goes into m' and what that is. Is that "m prime"? I would appreciate some advice on what he is doing here?

Thank you

Zev Chonoles
  • 129,973
tridianprime
  • 141
  • In an answer to your prior question, I rewrote the proof in positive form, i.e. using complete induction (vs. infinite descent). I suspect that you'll find the proof clearer in this form. – Key Ideas May 26 '13 at 18:16

1 Answers1

0

No, $m'$ is not intended to be prime.

This is a proof by contradiction; we temporarily assume that our goal (every positive integer has a unique prime factorization) is false, and then show that it being false leads to a contradiction, therefore implying that it must have been true.

So, we assume that there exists some positive integer that has two different prime factorizations. The collection of all positive integers with two different factorizations, being non-empty, has a smallest element; we let $m$ be this smallest element. Thus, any positive integer smaller than $m$ will have a unique factorization.

We are constructing an number $m'$ that will be be a positive integer and smaller than $m$, so that it has only one prime factorization; by studying the prime factorization of $m'$, we can reach a contradiction (like we wanted to).

Zev Chonoles
  • 129,973
  • Thank you, but why does m' then equal what it does. Why does it equal m-($p_1$$q_2$...$q_s$). Also, why is $p_1$ before al of the $q$'s. – tridianprime May 26 '13 at 16:58
  • @tridianprime: We are defining $m'$ ourselves; this is a number that is useful in the proof, so we give it a name. We assumed at the beginning of the proof that $$q_1\leq q_2\leq\cdots\leq q_s$$ and then further assumed that $p_1<q_1$. – Zev Chonoles May 26 '13 at 17:12
  • I get that but what is the point in m'=m-(p1q2...qs) and why is $p_1$ in with the q's. – tridianprime May 26 '13 at 17:19
  • @tridianprime there is not a philosophical reason for $m'$ to have that form, it is simply a guess, the fact that the proof actually works will show that that was the right guess – Federica Maggioni May 26 '13 at 17:24
  • I'm very confused. As a guess they put m'=m-(p1q2...qs) and put p1 in front of q2...etc.? – tridianprime May 26 '13 at 17:27
  • @tridianprime that definition of $m'$ serves to make $m'$ positive and smaller than $m$, while $p_1$ at first place is only convenience for collecting it in equation (3), but as you know multiplication is commutative, hence the place of factors is irrelevant – Federica Maggioni May 26 '13 at 17:35
  • I'm sorry but I really am lost now. How can you just put $p_1$ in first place. It is not equal to $q_1$ but instead is greater than? – tridianprime May 26 '13 at 17:42
  • @tridianprime: You rearrange/relabel them if necessary. Do you understand the statement: "given any two real numbers $a$ and $b$, without loss of generality we have $a\leq b$"? Either $a<b$, or $a=b$, or $a>b$. If $a>b$, just swap the names of the numbers. Another way of thinking about it: given any two real numbers, one will be less than or equal to the other. Give the name "$a$" to the former, and the name "$b$" to the latter. – Zev Chonoles May 26 '13 at 17:43
  • yes, but it was $p_1$ < $q_1$ and not <= – tridianprime May 26 '13 at 17:46
  • Are you referring to m and m' or to $p_1$ and $q_1$. – tridianprime May 26 '13 at 17:47
  • @tridianprime: He explains that in the argument. Look at the paragraph beginning "Now $p_1$ cannot be equal to $q_1$, for if it were..." – Zev Chonoles May 26 '13 at 17:48
  • Then why can I treat $p_1$ to be the same as $q_1$ and have ($p_1$$q_2$...$q_s$)? – tridianprime May 26 '13 at 17:49
  • You are not treating $p_1$ the same as $q_1$. You have numbers $p_1$, $q_2,\ldots,q_s$, and you can form their product. You are allowed to write down any number you want. – Zev Chonoles May 26 '13 at 17:50
  • let us continue this discussion in chat – tridianprime May 26 '13 at 17:51