Let $$T=\{n | 0,1~\mathrm{do~not~occur~in~the~decimal~expansion~of~n}\}$$
I'll make this Conjecture: $T\cap S$ is finite.
That is, there are only finitely many $n$ that don't have the digit 1 in their decimal representation and that have $P^\infty(n)>0$.
The case where all of the digits are the same (and not 1) is covered by a long-standing conjecture of Furstenberg (Conjecture 2' on page 25 of this paper I cited in my answer to this tangentially related question), which says that large enough powers of any number (not a power of 10) contain any finite pattern of digits.
In particular for this problem, for $2\le d \le 9$ there is a $K(d)$ large enough such $d^k$ has a zero in its decimal expansion for $k>K(d)$ and so the decimal numbers $n=ddd\cdots d$ with $k$ repeated $d$s have $P^2(n)=0$.
I think this can be generalized to the case where different digits are allowed, but I only have a very abstract argument. All patterns of digits appear in large powers of $d_1$ because the decimal representation for $d_1^{k_1}$ is "random" in some sense, and multiplying by another $d_2^{k_2}$ gives something else that is still random (unless 10 divides $d_1\times d_2$). So for $k_1+k_2$ large enough $n=d_1^{k_1}d_2^{k_2}$ will contain a zero in its decimal expansion. And continuing the argument, for $k_1+k_2+k_3+k_4$ large enough every $n\in T$ with
$$
P(n)=2^{a_1}3^{a_2}4^{a_2}5^{a_2}6^{a_2}7^{a_2}8^{a_2}9^{a_2} = 2^{k_1}3^{k_2}5^{k_3}7^{k_4}
$$
will contain a zero in its decimal expansion and will have $P^2(n)=0$.
A computer check of exponents up to 200 suggests that the largest value $k_1+k_2+k_3+k_4$ can take is 44, and the largest $n\in T$ with $P^\infty(n)\ne 0$ have $P(n)=2^{39}3^3 7^2$.
Let $L(n)$ be the number of digits in the decimal representation of $n$.
Given $n\in T$ with $L(n)<N$, we can mix the digits of $n$ with $N-L(n)$ additional 1 digits to get $N$-digit numbers $n_1,n_2,\dots$ with $P(n)=P(n_1)=P(n_2)=\cdots$. For example, let $n=2677,N=10$, and
$$
n_2=1111112677, n_2=1111771216, n_3=7172611111, \ldots \\
P(n)=588=P(n_1)=P(n_2)=P(n_3)=\cdots
$$
If the number distinct permutations of the digits of $n$ is $L(n)!/R(n)$, then the number of ways we can generate $N$-digit numbers from $n$ this way is
$$
c(n,N) = \frac{N!}{(N-L(n))!R(n)} = \frac{N^{L(n)}}{R(n)}-O(N^{L(n)-1})
$$
In our example $c(2677,N)=N^4/2-O(N^3)$.
Operating under the conjecture that $L(n)$ is bounded for $n\in T\cap S$, for large $N$ the $N$-digit numbers in $S$ will be mainly composed of $1s$, and their count will be dominated by $N^{L(n)}$ for the longest $n$s.
My computer search turned up the longest $n$ as follows:
$$
\begin{array}{c|c|c|c}
P^\infty(n) & P(n) & L(n) & c(n,N) \\
\hline
2 & 2^{26}3^3 & 29 & N^{29}/(2.4\times 10^{27}) \\
3 & 3 & 1 & N \\
4 & 2^{23}3^7 7 & 31 & N^{31}/(1.3\times 10^{26}) \\
5 & 3^5 5 7^2 & 8 & N^8/240\\
6 & 2^{24} 3^6 7^6 & 36 & N^{36}/(3.2\times 10^{29}) \\
7 & 7 & 1 & N \\
8 & 2^{39} 3^3 7^2 & 44 & N^{44}/(2.4\times 10^{47})\\
9 & 3^2 & 2 & N^2/2
\end{array}
$$
where the right column gives the asymptotic behavior for very large $N$. There is also only one $N$-digit number consisting of all 1s with $P(n)=1$.
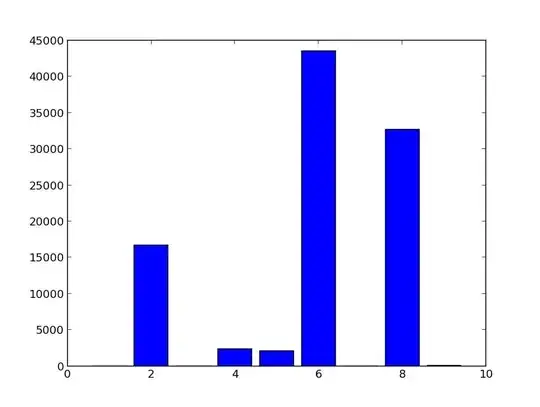
So even though up to 50 million the histogram shows a pattern similar to yours:
$$
\begin{array}{c|c|c|c|c|c|c|c|c|c}
P^\infty & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\
\hline
\mathrm{count} & 8 & 317446 & 36 & 27070 & 16325 & 1336881 & 35 & 697581 & 119
\end{array}
$$
my results suggest that eventually $P^\infty=4$ will dominate $P^\infty=2$, and in the large $N$ limit almost all of $S$ will be made up of numbers with thirty-nine 2s, three 3s, two 7s and a large number of 1s, each with $P^\infty=8$.