How to prove that
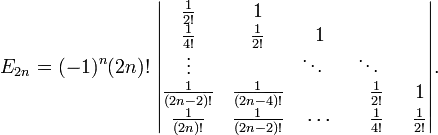
where $\ E_{2n}$ is the $2n^{th}$ euler number
and $$\frac{1}{\cosh(x)}=\sum_{n=0}^{\infty }\frac{E_n}{n!}x^n$$
Is there maybe some link with an answer, or a book in which the above is shown?
Asked
Active
Viewed 170 times
3
-
:whats source ? – M.H May 23 '13 at 18:30
-
@MaisamHedyelloo in the same link (http://en.wikipedia.org/wiki/Euler_number) – mnsh May 23 '13 at 18:32
-
A related problem. – Mhenni Benghorbal May 24 '13 at 06:08
-
@MhenniBenghorbal:if you can give me an answer because from 4 month to now and I didnt find way to solve the question – mnsh Oct 10 '13 at 09:25
1 Answers
1
We have $\cosh (x) \cdot \frac{1}{\cosh (x)} = 1$ and $\cosh (x) = \sum_{k=0}^\infty \frac{1}{2k!}x^{2k}$. Multiplying and taking the coefficient of $x^{2n}$ we arrive at $E_0 = 1$ and $\sum_{k=0}^n \frac{1}{2k!}\cdot\frac{E_{2n-2k}}{(2n-2k)!} = 0$ for $n \geq 1$. From here on this is a straight forward proof by induction.
Alexander Thumm
- 5,112