Can the Stern-Brocot tree be employed for better convergence of $2^m/3^n$?

Question

Prerequisite reading:

1. Can any positive real be approximated as $2^m/3^n$ with $(m,n)$ large enough?
2. Stern Brocot tree sequence

Something unsatisfactory is going on with convergence of $\,2^m/3^n\,$ towards a positive real $\,r\,$. As soon as we have reached sufficient approximation, the next step in our current iteration procedure is to increase $\,m \to m+1\,$ if $\,2^m/3^n < r\,$ or to increase $\,n \to n+1\,$ if $\,2^m/3^n > r\,$. But then we have actually destroyed our approximation so far, according to $\,2^m/3^n \to 2.2^m/3^n\,$ or $\,2^m/3^n \to 2^m/3^n/3\,$ respectively. Thus it looks like we are starting all over every time again without making much progress. The number of iterations needed indeed is very large.
Reason why I have been looking for a procedure that does not have this drawback, i.e. where the next approximation is always closer to the desired outcome. This is what I have tried so far.

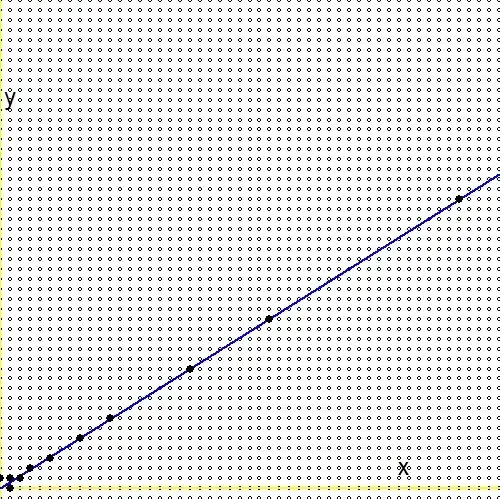
According to question (2.), for every positive real number $0 \lt g \lt 1$ , there exists an infinite sequence in the Stern Brocot tree [ .. ] that converges to the real number. Meanwhile, this question has an answer, and the main result in there reads as follows: $$ - \frac{1}{n_1(n_1+n_2)} \lt g - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} $$ In view of question (1.), we substitute $\ln(2)/\ln(3)$ for that number $g$. Then it follows that: $$ - \frac{1}{n_1(n_1+n_2)} \lt \frac{\ln(2)}{\ln(3)} - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} \\ - \frac{\ln(3)}{n_1} \lt \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \lt + \frac{\ln(3)}{n_2} \\ \ln\left(3^{-1/n_1}\right) \lt \ln\left(\frac{2^{n_1+n_2}}{3^{m_1+m_2}}\right) \lt \ln\left(3^{+1/n_2}\right) \\ 3^{-1/n_1} \lt \frac{2^{n_1+n_2}}{3^{m_1+m_2}} \lt 3^{+1/n_2} $$ The search through the Stern-Brocot tree can be pictured. The blue line is the function $\,\color{blue}{x\ln(2)-y\ln(3)=0}\,$, small circles are fractions, mapped on a grid $\,m/n \to (m,n)\,$, massively black filled dots are the fractions in the Stern-Brocot tree. It is seen that searching through the tree is much more efficient than increasing $m$ and $n$ with increments one at a time.

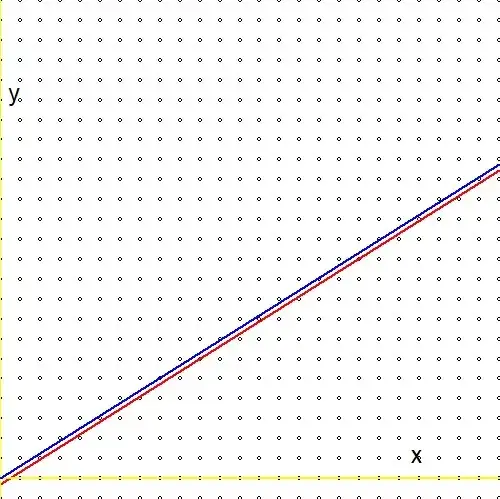
Now compare the expression at the second line of the above formulas with an analogous expression in reference (1.): $$ \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \quad \Longleftrightarrow \quad m\ln(2) - n\ln(3) - \ln(r) $$ And be prepared for a disappointment: the logarithm of the arbitrary real $r$ is missing! Or alternatively: $\ln(r)=0$ or $r=1$. This means that our "infinite search" through the Stern-Brocot tree, though highly efficient, finally arrives at an approximation only for the number one. I find this weird, because - graphically - there doesn't seem to be a great difference between $\color{red}{2^m/3^n \to r}$ and $\color{blue}{2^m/3^n \to 1}$:

Hence the QUESTION: does there exist a means for adapting the Stern-Brocot procedure such that it works for reals other than one?

EDIT.

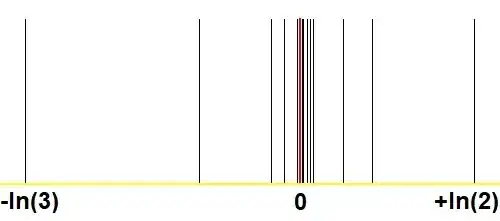
Here comes another graph that shows the astonishing convergence with the Stern-Brocot method, in comparison with analogous pictures in my Q & A   Can any positive real be approximated as $2^m/3^n$ with $(m,n)$ large enough? :

Answer 1

I will give an approach which doesn't use the Stern-Brocot procedure.

It suffices to show that $\frac{2^{m}}{3^{n}}$ is dense in the interval [1,2]. Since taking $\alpha\in (0,\infty)$ outside this interval there is some $k\in Z$ so that $\alpha = 2^{k}\gamma $ for some $\gamma \in [1,2]$. Then we know there is a sequence in $\frac{2^{m}}{3^{n}}$ which approaches $\gamma$, multiplying the sequence termwise by $2^{k}$ (possibly taking a tail of the sequence), we get a sequence in $\frac{2^{m}}{3^{n}}$ which approaches $\alpha$.

Next consider that the map $f:[1,2] -> [0,1]$ with $f(x) = log_{2}(x)$ is a bijection.

The image of $\frac{2^{m}}{3^{n}}$ under the map is $N-Nlog_{2}(3)$. So it is enough to show that $N-Nlog_{2}(3)$ is dense in $[0,1]$.

This is a consequence of Weyl's Equidistribution theorem, which is a special case of the Ergodic theorem.

Consider $a=2-log_{2}(3) = log_{2}(\frac{4}{3})$, so $a$ is in the image of the set, So is $na = log_{2}(\frac{4^{n}}{3^{n}})$ and so is the fractional part of $na$.

The weyl Equidistribution theorem (which is not a trivial result) shows that for irrational a the fractional part of $na$ is uniformly distributed and hence dense on [0,1]. Since $2-log_{2}(3)$ is irrational you can use this theorem.