Probability that $n$ random walks (1D) intersect a single point

Question

I am struggling finding a relation to determine the probability $n$ random walks (1D) intersect in a single point at step $s$. In the method below my attempts. My method is somewhat intuitive based. I am looking for more rigorous proof.

note: This question arises from someone who claims that a matching cumulative digit sum of: $\pi$, $e$ and $\varphi$ (golden ratio) is unique and "cosmological" [1]. I tend to disprove it. This digit sum can be seen as a random walk if the constants are normal (every digit occurs with same frequency).

Method:

For every step $s$ on the random walk we can determine the probability density function if we know the standard deviation on every step $s$.

The standard deviation of a single step can be calculated it's a discrete uniform distribution "equally likely outcomes", where $q$ is the number of outcomes e.g. the number of digits $[0,1,2,3,4,5,6,7,8,9]$, $q=10$:

$$\sigma=\sqrt{\frac{q^{2}-1}{12}} $$

All the (1D) random walks start in the origin for this example. The standard deviation will grow with every step $s$, the variance is proportional to the number of steps [2].

$$Var(s)=s \cdot \sigma^{2}$$

$$\sigma(s)=\sqrt{s} \cdot \sigma$$

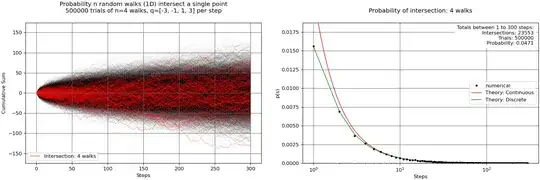
While the bins grow rapid I assume a normal approximation of the Binomial distribution.

$$f(x)=\int_{-\infty}^{\infty} {\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x}{\sigma }}\right)^{2}}dx $$

The probability that $n$ random walks intercept in a single point is (not sure):

$$p(s)=\int_{-\infty}^{\infty} \left[ {\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x}{\sigma }}\right)^{2}} \right]^n dx $$

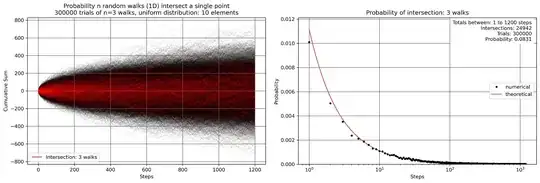
With help of Wolfram Alpha [3] the solution is found for $n=3$ meaning the probability of $3$ point intersecting random walks.

$$p(s)=\frac{1}{2 \sqrt{3} \ \pi \ \sigma^{2}} \cdot \frac{1}{s}$$

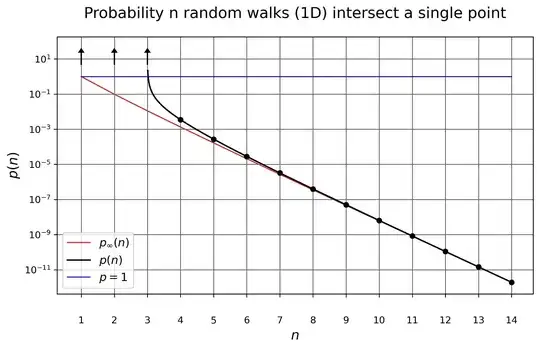
The total probability $p(n)$ is proportional to the reciprocal sum of $s$. So the total probability is proportional to the harmonic series:

$$p(n)=\frac{1}{2 \sqrt{3} \ \pi \ \sigma^{2}} \cdot \sum_{s=1}^{\infty}\frac{1}{s}$$

This series diverges, meaning there are infinate point intersections of $n=3$ random walks. So a matching cumulative digit sum of $\pi$, $e$ and $\varphi$ is not unique, probability $\sim 8 \%$ for the first 1200 digits (see graph).

Question

Does anyone know the general formula for the probability $p(n)$ that $n$ random walks (1D) intersect a single point?

import numpy as np
#Elements of digits [0,1,2,3,4,5,6,7,8,9] rescaled to fit random walk
array=[-9,-7,-5,-3,-1,1,3,5,7,9]
#steps, in single random walk, x walks to intercept, number of trial to find intercept
steps=2500
xwalks=3
trials=1500
#Set output array to zero
count=np.full([steps],0)
for n in range(trials):
#Identify initial array, set total array to zero
w0=np.random.choice(array,steps)
w0=np.cumsum(w0)
total=np.full([steps],0)

#Select x random walk check for intercept
for m in range(xwalks-1):

    #Next current random walk
    w=np.random.choice(array,steps)
    w=np.cumsum(w)

    #Compare previous and current random walk
    eq=np.equal(w0,w)
    eq=eq.astype(int)

    #Count intercepts
    total=total+eq

    #Set current walk to previous
    w0=w

#Sum all interceptions for all trials
count=count+np.where(total==(xwalks-1),1,0)


#Print output
print(count)
print(np.sum(count))
print(np.sum(count)/trials)

Answer 1

The probability $n$ random walks starting in origin (1D) intersect a single point can be calculated with:

$$p(s)=\int_{-\infty}^{\infty} \left[ {\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x}{\sigma }}\right)^{2}} \right]^n dx$$

Solutions have been found with Wolfram Alpha 1. This solution can be written as a function of the number of steps $s$. So the probability $p$ at $s$ steps can be calculated with a empirical found formula:

$$p(s)= \frac{1}{g(n) \cdot \sigma ^{(n-1)} } \cdot s^{-\frac{1}{2}(n-1)} $$

Where the function for $g(n)$ is found as:

$$g(n)=\sqrt { n} \cdot (2 \pi)^{\frac{1}{2}(n-1)}$$

The total probability over all steps $s$ is only dependent upon the $p$-series formed by $s$. This summation can be calculated with the Riemann zeta function:

$$\zeta(\small{\frac{1}{2}(n-1)} \normalsize) =\sum\limits_{s=1}^{\infty}s^{- \frac{1}{2}(n-1)}$$

$$p(n)=\frac{1}{g(n) \cdot \sigma^{(n-1)}} \cdot \sum\limits_{s=1}^{\infty}s^{- \frac{1}{2}(n-1)} $$

Graph information

Below a table and a plot for the probabilities of $p(n)$ point coinciding random walks (1D). Details:

• The standard deviation is chosen: $10$ equal likely outcomes per step: $$\sigma=\sqrt{\frac{99}{12}}$$
• For infinate random walks $n\rightarrow \infty$ the $p$-series converges to $1$. This probability is plotted as: $p_{\infty}(n)$.
• $p(n)$ can be graphed as an continuous function.
• Values $n<3$ have not been graphed while Riemann zeta $\zeta(<1)$ are resulting in negative probabilities.

Observations:

• $n=3$ random walks have infinate single point intersections. $p$-series: $\sum\limits_{s=1}^{\infty}s^{-1}=\infty$, Riemann zeta: $\zeta(1)=\infty$ both have infinity probability $p(n)\rightarrow \infty$.
• $n=2$ random walks have infinate single point intersections for $p$-series: $\sum\limits_{s=1}^{\infty} s^{-\frac{1}{2}}=\infty$ , interpretation Riemann zeta is unclear: $\zeta(\frac{1}{2})=-1.46035...$ resulting in a negative probability $p(2)$.
• It is possible that $n\geq4$ random walks never point intersect. For $n=4$ only $\sim 0.35 \%$ of them will point intersect (with 10 equal likely outcomes per step).
• The probability $p(n)$ plot of $n$ random walks (1D) intersecting a single point is directly related to the $p$-series. A relation with Riemann zeta is unclear while the number of walks $n=a+ib$ would be a complex number.
• I learned this has to do with: recurrence and transience 2.

Any more rigorous proofs or information is welcome please.

Answer 2

I am looking at this problem without any prior assumed knowledge of random walks, so I am not sure whether or not my analysis is useful - it might offer some fresh perspectives or just cover ground which is already known.

Firstly, it might make sense to consider the binary representation of the numbers in question to simplify matters. Then the probability that n random walks intersect at a single point after m steps/digits is p[m,n]=Sum[(nCi/2^m)^n,{i,1,m}] using pseudo-Mathematica syntax.

The probability that n random walks intersect at a single point at any step in the future is Sum[p[m,n],{m,1,infinity}].

Note that p[m,n] vanishes to zero as m increases towards infinity. This means that the probability of n random walks intersecting also vanishes to zero.

In fact, it is known that if we have two possible binary digits 0 and 1, then the expected value of the sum of the binary digits is 1/2 multiplied by the number of digits, and the standard deviation is proportional to the square root of the number of digits. (Consider the absolute value of the deviation from the expected value, for example, which makes more intuitive sense.) Therefore, for n different random or pseudorandom irrational numbers such as pi, we would expect the digit sums to diverge (even though the expected digit sums are the same), and therefore I actually agree with the person who suggested that each random or pseudorandom number has an unique digit sum footprint. This concurs with the fact that the probabilities vanish to zero.

---

Alternatively, instead of considering an one dimensional random walk, we can consider a n dimensional random walk.

To demonstrate this, first consider a 2D random walk for the case n=2. Instead of consider the binary digits 0 or 1, consider the digits to be either -1 or 1, which is the standard form of the random walk usually considered. To convert between binary digits 0 or 1 and -1 or 1, a translation and scaling factor can be applied.

With each step, we can go either in the positive or negative direction for each of the two dimensions, so we are essentially travelling diagonally in the plane with each step. For the two random walks to intersect after m steps, we look at the points (x,x) along the diagonal of the plane i.e. (0,0), (1,1), (-1,-1), (2,2), (-2,-2) etc.

By applying a 45 degree (or pi/4 radian) rotation followed by scaling by a factor of 1/Sqrt[2], the problem can be restated so that at each step, we are moving either left, right, up or down, and for the two random walks to intersect after m steps, we are now looking at the points (x,0) along the negative/positive x-axis.

This can now be extended beyond two dimensions to n dimensions.

Answer 3

After studying I think I answered my own question. The method has similarities corresponding with: SE.

In my earlier answer I demonstrated how to determine the probability of $n$ intersecting random walks with $2$ or more likely outcomes per step. The method used a normal approximation making an error in the probability for small numbers of steps.

The probability of intersection for small number of steps can be calculated with an discrete method. By using generating functions, a solution is found and is based upon: SE.

The probabilities of a single random walk at step $s$ is determined by the coefficients of the generating function below. Where $d$ is the number of equal likely possibilities per step e.g. $d=2$ for random walk: $[-1,1]$:

$$\left( \frac{1}{d}x^{0}+\frac{1}{d}x^{1}+\frac{1}{d}x^{2}...+\frac{1}{d}x^{d-1} \right)^{s}=\frac{1}{ d^{s}} \left( \frac{1-x^{d}}{1-x} \right)^{s}$$

The coefficients can be calculated by applying the generalized binomial theorem. Where $n$ is the number of intersecting random walks. $p(s)$ is the total probability for an intersection occurring on step $s$:

Discrete method, $s<20$: $$\boxed{p(s)=\sum_{i=0} \left[\frac{1}{d^s} \sum_{r=0} (-1)^{r} \binom{s}{r} \binom{s+i-dr-1}{i-dr} \right]^{n}}$$

The discrete method is realistic for $s<20$ steps. For more than $s\geq20$ the normal approximation is more efficient.

$$p(s)=\int_{-\infty}^{\infty} \left[ {\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x}{\sigma }}\right)^{2}} \right]^n dx$$

An empirical formula was found see; my question and first own answer (confirmation here: SE). The standard deviation is determined from a discrete uniform distribution, growing with $\sqrt{s}$ per step while a random walk SE:

Continuous method, $s\geq20$: $$\sigma=\sqrt{\frac{(d^{2}-1)}{12}}$$ $$\boxed{p(s)= \frac{1}{\sqrt { n} \cdot (\sigma \sqrt{2 \pi})^{(n-1)} } \cdot s^{-\frac{1}{2}(n-1)}} $$

Both functions: discrete and continuous have been verified in a simulation. The intersections of $n=4$ random walks where counted. Random walks were used with $d=4$ equal likely outcomes per step $[-3,-1,1,3]$. The graphs show the discrete method is practical and accurate for $s<20$ the normal approximation is useful for $s\geq20$.

---

Finally, I want to summarize that the total probability: the sum over all steps $p(n)$ can be calculated by using the $p-$series (or Riemann Zeta function):

$$p(n)=\frac{1}{\sqrt { n} \cdot (\sigma \sqrt{2 \pi})^{(n-1)} } \cdot \sum\limits_{s=1}^{\infty}s^{- \frac{1}{2}(n-1)}$$

$$p(n)=\frac{1}{\sqrt { n} \cdot (\sigma \sqrt{2 \pi})^{(n-1)} } \cdot\zeta(\small{\frac{1}{2}(n-1)} \normalsize) $$

For $n\leq3$ point intersecting random walks the series diverges resulting in infinite intersections. For $n\geq4$ the series converges resulting in finite number of intersections. This recurrence and transience is also seen with random walks returning to the origin (one more degree of freedom) and related to Markov processes.

Interesting is that $n=2$ intersecting random walks coincides with the critical line on the Riemann Zeta function.

Answer 4

I now realise that your rebuttal of my analysis in your comment above at Probability that $n$ random walks (1D) intersect a single point was in fact valid, as I had made a mistake in my analysis. I assumed incorrectly that I could simply add together the probabilities of collision after one step, two steps etc. to get the total probability of collision. However, these events are not mutually exclusive, since random walks can collide at multiple steps, so if the probability of collision at step 1 was 0.6 and the probability of collision at step 2 was 0.5, I would already have a probability exceeding 1. Hence, the correct process is to work out the probability of non-collision before step m multiplied by the probability of collision at step m, and only then add together the probabilities. Alternatively, I could just calculate the probability of non-collision at or before step m by multiplying together probabilities, then subtract it from one, and take the limit as m tends to infinity.

---

Edit:

This method describes collision random walk with probability per step is: [-1,1] 50%.

s: step number in random walk, n: number of intersecting random walks.

Probability intersecting at single step position: $$p(s)= \sum_{k=0}^{s} \left(\frac{1}{2^{s}} \binom{s}{k}\right)^{n}$$

Total probability over all steps: $$p(n)=\sum_{s=1}^{\infty}\sum_{k=0}^{s} \left(\frac{1}{2^{s}} \binom{s}{k} \right)^{n}$$

---

I have now created a spreadsheet to calculate the answer to your question, which is:

n	p(n)
1	1
2	1
3	0.907472937
4	0.382922701
5	0.147129979
6	0.062758395
7	0.028516044
8	0.013419184
9	0.006446336
10	0.003136593
11	0.001538874
12	0.000759198

I am not sure how accurate my results are, but if you need better accuracy, you could extend the spreadsheet tables as required.

My spreadsheet uses data tables, and it appears that Excel cannot handle nested data tables, so the table above was produced by manually typing in the first twelve input values for n and copying the result. For a larger data set, a quick script could be written to automate the process.

The spreadsheet is available at https://groups.io/g/UnsolvedProblems/message/12251.

I can now see that your question is related to Pólya's Random Walk constants, but because you are essentially asking a different question, I don't think the answer to your question should directly equate to Pólya's Random Walk constants.

In terms of the normal approximation you mentioned in your analysis, the conditions of the Central Limit Theorem state under which circumstances a normal approximation applies, which can be found at https://en.wikipedia.org/wiki/Central_limit_theorem.