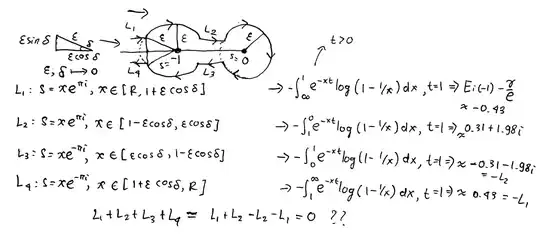Is The Inverse Laplace Transform of $e^{st}\operatorname{Log}\left(\frac{s+1}{s}\right)$ doable using inversion formula?

Question

I'm trying to solve inverse laplace transform using inversion formula and given by this integral: $$\frac{1}{2\pi i}\int_{\gamma-i\infty}^{\gamma+i \infty} e^{st}\operatorname{Log}\left(\frac{s+1}{s}\right)\,\Bbb ds.$$

Here is my contour, since the branch points of $\operatorname{Log} \left(\frac{s+1}{s}\right)$ are $0$ and $-1$

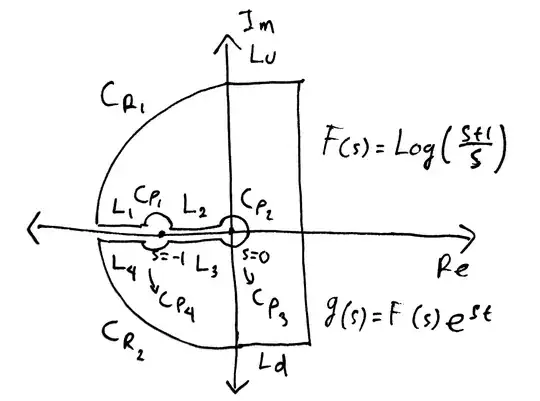
First, i want to show integral on $L_u\cup L_d$ is $0$ by bounding the integral with ML and then take the limit when $R$ goes to $\infty$.

By letting $L_u,\, L_d: s= \xi\pm iR,0\leq \xi\leq \gamma$, where $\gamma$ is the real number that the vertical line of the given contour passed by.

Since the $L$ is $\lvert e^{t(\xi\pm iR)} \rvert$, then i have ML inequality as below:

$$\lvert F(s)e^{st} \rvert \leq M_R \lvert e^{t(\xi\pm iR)} \rvert = M_R e^{\xi t} \leq M_R e^{at}$$

Next, i need to find $M_R$ and take the limit. $$\begin{align} \left|F(s)\right| &= \left|\operatorname{Log}\left(\frac{s+1}{s}\right)\right|\\ &= \left|\operatorname{Log}\left(\frac{\xi\pm iR+1}{\xi\pm iR}\right)\right| = M_R \end{align}$$

And by taking the limit of the last expression when $R$ goes to infinity yields $0$. Meaning the integrals along those lines are $0$.

So, from here, am i doing this right? I'm not sure my work is correct. Maybe there are some mistakes there. Help me please!

Edit: Working with my $L_u$ with $ML$ inequality, i have $L=\gamma$. Assuming $-\pi<\operatorname{arg}{s}\leq \pi$ and parametrizing $s=-\xi+iR$, $\xi\in [-\gamma,0]$:

$\begin{align} \left|\int_{L_u}\right| &\leq \left|e^{st} \log\left(1 + \frac 1s\right)\right|\\ &\leq \left|e^{-\xi t}\right| \left|e^{iRt}\right|\left|\ln\left|1+ \frac{1}{-\xi+iR}\right| + i\pi\right|\\ &\leq 1\cdot 1 \cdot \ln\left(1+\frac 1R\right) + \pi\\ &\approx \frac 1R + \pi \end{align}$

Combining the $ML$ i have $$\frac{\gamma}{R} +\gamma\pi$$ Which does NOT approach to $0$. Why? Please spot my mistake. I can't think about how to make it goes to $0$ since yesterday. Hope you kind to help me.

New Edit: Now my main question is not about ML. I managed to set the big and small arc goes to $0$. My main question now is "is it possible to evaluate this by using inversion formula (without differentiate both sides) and use log form instead?"

What i mean by differentiate both sides is: $$\begin{align} \mathcal{L}^{-1} &= \operatorname{Log}\left(\frac{s+1}{s}\right)\\ (\mathcal{L}^{-1})' &= \frac{1}{1+s} - \frac{1}{s} \end{align}$$

I don't want this kind of solution. What i really want is evaluating $\operatorname{Log}\left(\frac{s+1}{s}\right)$ by inversion formula. That's it. because I keep getting integrals on the contour lines above and below the branch cut cancel each other and make everything 0, which of course I don't want it.

Attempt:

Answer 1

$\newcommand{\bbx}[1]{\,\bbox[15px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\on}[1]{\operatorname{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ $\ds{\LARGE\left. a\right)}$

One idea, in this particular case, is to get rid of the $\ds{\ln}$-function by introducing an integral representation of it. Namely, \begin{align} &\bbox[5px,#ffd]{\left.{1 \over 2\pi\ic} \int_{\gamma\ -\ \ic\infty}^{\gamma\ +\ \ic\infty} \expo{st}\ln\pars{s + 1 \over s} \,\dd s\,\right\vert_{\,\gamma\ >\ 0}} \\[5mm] = &\ \int_{\gamma\ -\ \ic\infty}^{\gamma\ +\ \ic\infty} \expo{st}\ \overbrace{\int_{0}^{1}{\dd x \over x + s}} ^{\ds{\ln\pars{s + 1 \over s}}}\ \,{\dd s \over 2\pi\ic} \\[5mm] = &\ \int_{0}^{1}\int_{\gamma\ -\ \ic\infty}^{\gamma\ +\ \ic\infty} {\expo{st} \over s + x}\,{\dd s \over 2\pi\ic}\,\dd x \\[5mm] = &\ \int_{0}^{1}\bracks{t > 0}\expo{-xt}\,\dd x = \bbx{\bracks{t > 0}\,{1 - \expo{-t} \over t}} \\ & \end{align}

---

$\ds{\LARGE\left. b\right): {\large Contour Integration}}$'

Note that $\ds{{s + 1 \over s} < 0}$ whenever $\ds{s \in \pars{-1,0}}$: It indicates that the $\mbox{$\ds{\ln}$-branch-cut}$ lies along $\ds{\bracks{-1,0}}$. Also, $\ds{{s \pm \ic\epsilon + 1 \over s \pm \ic\epsilon} \,\,\,\stackrel{{\rm as}\ \epsilon\ \to\ 0^{+}}{\sim} \,\,\, \pars{1 + s \over s} \mp {\epsilon \over s^{2}}\,\ic}$ such that the $\ds{\ln}$-$\ds{arg}$ is $\pars{-\pi}$ when $\ds{s}$ is above the real axis and $\ds{\pi}$ when it's below the real axis. \begin{align} &\bbox[5px,#ffd]{\left.{1 \over 2\pi\ic} \int_{\gamma\ -\ \ic\infty}^{\gamma\ +\ \ic\infty} \expo{st}\ln\pars{s + 1 \over s} \,\dd s\,\right\vert_{\,\gamma\ >\ 0}} \\[5mm] = &\ -\int_{-\infty}^{-1}\ln\pars{s + 1 \over s}\expo{ts} {\dd s \over 2\pi\ic}\label{1}\tag{1} \\[2mm] - &\ \int_{-1}^{0}\bracks{\ln\pars{-s - 1 \over s} - \ic\pi}\expo{ts} {\dd s \over 2\pi\ic} \\[2mm] - &\ \int_{0}^{-1}\bracks{\ln\pars{-s - 1 \over s} + \ic\pi}\expo{ts} {\dd s \over 2\pi\ic} \\[2mm] - & \int_{-1}^{-\infty}\ln\pars{s + 1 \over s}\expo{ts} {\dd s \over 2\pi\ic}\label{2}\tag{2} \end{align} I included (\ref{1}) and (\ref{2}) "by completeness" but, indeed, it's not necessary because the $\ds{\ln}$-branch-cut lies along $\ds{\bracks{-1,0}}$ albeit it guarantees the vanishing out of the integration along the"big-arc".

Then, \begin{align} &\bbox[5px,#ffd]{\left.{1 \over 2\pi\ic} \int_{\gamma\ -\ \ic\infty}^{\gamma\ +\ \ic\infty} \expo{st}\ln\pars{s + 1 \over s} \,\dd s\,\right\vert_{\,\gamma\ >\ 0}} \\[5mm] = &\ -\int_{0}^{1}\bracks{\ln\pars{-s + 1 \over s} - \ic\pi}\expo{-ts} {\dd s \over 2\pi\ic} \\[2mm] &\ \,\, + \int_{0}^{1}\bracks{\ln\pars{-s + 1 \over s} + \ic\pi}\expo{-ts} {\dd s \over 2\pi\ic} \\[5mm] = &\ \int_{0}^{1}\expo{-ts}\,\dd s = \bbx{1 - \expo{-t} \over t} \\ & \end{align}

Answer 2

Let's pick a sufficiently large $\gamma$ such that $|s|>1$, so that we can plug in

$$ \log\left(1+\frac1s\right)=\sum_{k=1}^\infty{(-1)^{k+1}\over ks^k} $$

and get

$$ \begin{aligned} f(t) &={1\over2\pi i}\int_{\gamma-i\infty}^{\gamma+i\infty}\sum_{k=1}^\infty{(-1)^{k+1}e^{st}\over s^k}\mathrm ds \\ &=\sum_{k=1}^\infty{(-1)^{k+1}\over k}{1\over2\pi i}\int_{\gamma-i\infty}^{\gamma+i\infty}{e^{st}\over s^k}\mathrm ds \end{aligned} $$

Provided that

$$ \mathcal L\{t^{k-1}\}(s)={(k-1)!\over s^k} $$

we can deduce

$$ \begin{aligned} f(t) &=\sum_{k=1}^\infty{(-t)^{k-1}\over k!} \\ &=-\frac1t\left[\sum_{k=0}^\infty{(-t)^k\over k!}-1\right] \\ &={1-e^{-t}\over t} \end{aligned} $$

where the final step follows from the fact that

$$ e^z=\sum_{n=0}^\infty{z^k\over n!} $$