I am trying to find the Inverse Laplace of the following function:
$$ F(s) = \frac{\mathrm{e}^{-x b \sqrt{s}}}{ b (a - s)\sqrt{s}} $$
I really don't know where to start on this one as I have only used the tables to complete other Inverse Laplace Transforms and this is beyond anything I have seen.
Let's evaluate
$$f(t) = \frac1{i 2 \pi} \int_{c-i \infty}^{c+i \infty} \frac{1}{\sqrt{s} (a-s)} e^{-b \sqrt{s}} e^{s t} $$
with $a \gt 0$ and $b \in \mathbb{R}$. Note that we require that $c \gt a$.
Consider
$$\oint_C dz \frac{1}{\sqrt{z} (a-z)} e^{-b \sqrt{z}} e^{z t} $$
where $C$ is a keyhole contour as pictured below.
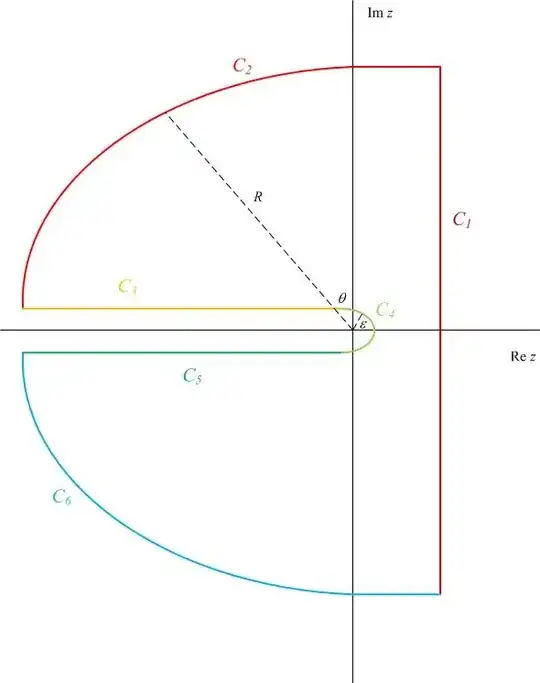
We will define $\text{Arg}{z} \in (-\pi,\pi]$, so the branch is the negative real axis. There are $6$ pieces to this contour, $C_k$, $k \in \{1,2,3,4,5,6\}$, as follows.
$C_1$ is the contour along the line $z \in [c-i R,c+i R]$ for some large value of $R$.
$C_2$ is the contour along a circular arc of radius $R$ from the top of $C_1$ to just above the negative real axis.
$C_3$ is the contour along a line just above the negative real axis between $[-R, -\epsilon]$ for some small $\epsilon$.
$C_4$ is the contour along a circular arc of radius $\epsilon$ about the origin.
$C_5$ is the contour along a line just below the negative real axis between $[-\epsilon,-R]$.
$C_6$ is the contour along the circular arc of radius $R$ from just below the negative real axis to the bottom of $C_1$.
We will show that the integral along $C_2$,$C_4$, and $C_6$ vanish in the limits of $R \rightarrow \infty$ and $\epsilon \rightarrow 0$.
On $C_2$, the real part of the argument of the exponential is
$$R t \cos{\theta} - b \sqrt{R} \cos{\frac{\theta}{2}}$$
where $\theta \in [\pi/2,\pi)$. Clearly, $\cos{\theta} < 0$ and $\cos{\frac{\theta}{2}} > 0$, so that the integrand exponentially decays as $R \rightarrow \infty$ and therefore the integral vanishes along $C_2$.
On $C_6$, we have the same thing, but now $\theta \in (-\pi,-\pi/2]$. This means that, due to the evenness of cosine, the integrand exponentially decays again as $R \rightarrow \infty$ and therefore the integral also vanishes along $C_6$.
On $C_4$, the integral vanishes as $\epsilon$ in the limit $\epsilon \rightarrow 0$. Thus, we are left with the following by the residue theorem (i.e., pole at $z=a$ inside $C$):
$$\begin{align}\left [ \int_{C_1} + \int_{C_3} + \int_{C_5}\right] dz \: \frac{1}{\sqrt{z} (a-z)} e^{-b \sqrt{z}} e^{z t} &= i 2 \pi \operatorname*{Res}_{z=a} \frac{1}{\sqrt{z} (a-z)} e^{-b \sqrt{z}} e^{z t}\\ &= -i 2 \pi a^{-1/2} e^{-b \sqrt{a}} e^{a t}\end{align}$$
Now, on $C_3$, we parametrize $z=x e^{i \pi}$ and the integral over that segment becomes
$$i \int_{\infty}^0 dx \frac{x^{-1/2}}{a+x} e^{-i b \sqrt{x}} e^{-x t} $$
On $C_5$, we parametrize $z=x e^{-i \pi}$ and the integral over that segment becomes
$$-i \int_0^{\infty} dx \frac{x^{-1/2}}{a+x} e^{i b \sqrt{x}} e^{-x t} $$
We add these two integrals to get
$$-i 2 \int_0^{\infty} dx \frac{x^{-1/2}}{a+x} \cos{\left (b \sqrt{x}\right )} e^{-x t} $$
The ILT is therefore
$$\frac1{i 2 \pi} \int_{c-i \infty}^{c+i \infty} \frac{1}{\sqrt{s} (a-s)} e^{-b \sqrt{s}} e^{s t} = \frac1{\pi} \int_0^{\infty} dx \frac{x^{-1/2}}{a+x} \cos{\left (b \sqrt{x}\right )} e^{-x t} - a^{-1/2} e^{-b \sqrt{a}} e^{a t}$$
The problem reduces to the evaluation of the integral on the RHS. Subbing $x=u^2$, we get
$$\frac{1}{\pi} \int_{-\infty}^{\infty} du \frac{\cos{b u}}{a+u^2} e^{-t u^2} $$
It turns out that this integral may be evaluated using an analog of Parseval's Theorem for Fourier transforms, which states that, given two functions $f$ and $g$, both $\in L^2(-\infty,\infty)$, and their Fourier transforms $F$ and $G$, respectively, the following relation holds:
$$\int_{-\infty}^{\infty} du \: f(u) \, g^*(u) = \frac{1}{2 \pi} \int_{-\infty}^{\infty} dk \: F(k) \, G^*(k)$$
In this case,
$$f(u) = e^{-t u^2} \cos{b u} \implies F(k) = \frac{\sqrt{\pi } \left(e^{-\frac{(b-k)^2}{4 t}}+e^{-\frac{(b+k)^2}{4 t}}\right)}{2 \sqrt{t}}$$
$$g(u) = \frac1{a+u^2} \implies G(k) = \frac{\pi}{\sqrt{a}} e^{-\sqrt{a} |k|} $$
The integral is now clearly expressible in terms of error functions. I will skip the messy algebra and leave it to the reader, but combining the final integral with the residue piece on the RHS, we get as the ILT $f(t)$:
$$\frac1{i 2 \pi} \int_{c-i \infty}^{c+i \infty} \frac{1}{\sqrt{s} (a-s)} e^{-b \sqrt{s}} e^{s t} = \frac{e^{a t}}{2 \sqrt{a}} \left [e^{b \sqrt{a}} \operatorname{erfc}{\left ( \frac{b+2 \sqrt{a} t}{2 \sqrt{t}}\right )} - e^{-b \sqrt{a}} \operatorname{erfc}{\left ( \frac{b-2 \sqrt{a} t}{2 \sqrt{t}}\right )}\right ] $$
$$ F(s) = \frac{\mathrm{e}^{-b \sqrt{s}}}{ (a - s)\sqrt{s}}=\frac{1}{2\sqrt{a}}\big(F_1(s)-F_2(s)\big) $$ $$F_1(s) = \frac{\mathrm{e}^{-b \sqrt{s}}}{ (\sqrt{s} + \sqrt{a})\sqrt{s}}$$ $$F_2(s) = \frac{\mathrm{e}^{-b \sqrt{s}}}{ (\sqrt{s} - \sqrt{a})\sqrt{s}}$$ From Bateman Tables of Integral Transforms (1954), p.247, Eq.(16),
the inverse Laplace transform of $F_1(s)$ is : $\mathrm{e}^{b\sqrt{a}+at }\operatorname{erfc}\big({\frac{b}{2\sqrt{t}}+\sqrt{at} }\big)$
the inverse Laplace transform of $F_2(s)$ is : $\mathrm{e}^{-b\sqrt{a}+at }\operatorname{erfc}\big({\frac{b}{2\sqrt{t}}-\sqrt{at} }\big)$
So, the inverse Laplace transform of $F(s)$ is : $$\frac{e^{a t}}{2 \sqrt{a}} \left [e^{b \sqrt{a}} \operatorname{erfc}\big({\frac{b}{2\sqrt{t}}+\sqrt{at} }\big) - e^{-b \sqrt{a}} \operatorname{erfc}\big({\frac{b}{2\sqrt{t}}-\sqrt{at} }\big)\right ] $$
There is a small discrepancy compare to the result of Ron Gordon (may be $t$ missing at the numerator in the erfc of his formula). But I could be wrong ?
Nevertheless, the beautiful calculus of Ron Gordon is admirable.
