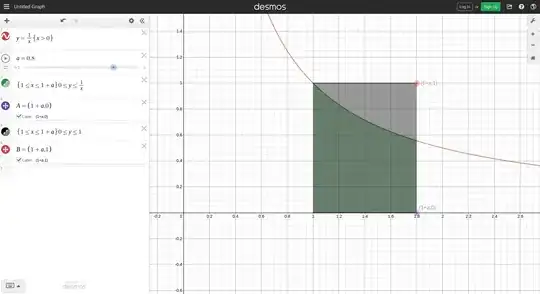
I want to prove $\log(1+x) < x.$
Of course, I can prove this by letting $f(x):= x - \log(1+x),$ and calculating $f'(x)$, ... .
But I wonder if I can prove this using Maclaurin's expansion.
$\log(1+x)=x-\dfrac{1}{2}x^2+\dfrac{1}{3} x^3-\cdots.$
The right-hand side includes the term "$x$" so it seems that I can use this equality in order to prove $\log(1+x) < x$, but I cannot.
I would like you to give me some ideas.
Since you talk about series expansions, one could exponentiate the inequality (the exponential function is monotonically increasing, so this is equivalent to the original inequality) to obtain $e^x > 1 + x$, which is easy to prove with the series expansion of the exponential function: we have $$e^x = 1 + x + \underbrace{x^2 + \ldots}_{> 0} > 1 + x$$ for all $x > 0$.
Take $0<x<1$, then if we let $a_k(x) = (-1)^{k+1}\frac{1}{k}x^k$ we see that $$\log (1+x)-x = \sum_{k=2}^{\infty}a_k(x).$$
Now note that in the specified interval we have that $|a_k(x)|>|a_{k+1}(x)|$ and that $\mathrm{sgn}\, a_k(x) = -\mathrm{sgn}\, a_{k+1}(x)$ so that the sum is alternating. These two properties implies that $a_{2k}(x)+a_{2k+1}(x)<0$ and therefore $$\log(1+x)-x= \sum_{k=2}^{\infty}a_k(x) = \sum_{k=1}^{\infty}\underbrace{a_{2k}(x)+a_{2k+1}(x)}_{<0}<0$$
For me the simplest proof is to look for the minimum value of $$f(x)=x- \log (1+x)$$ $$f'(x)=1-\frac 1{1+x} \qquad \text{and} \qquad f''(x)=\frac 1{x^2} \quad > 0~~\forall x$$ So the extremum is at $x=0$ and the second derivative test shows that this is a minimum. So, in real domain, $\forall x$ $$x \geq \log(1+x).$$
The definition of natural log in How can we come up with the definition of natural logarithm? allows a proof without words.
interactive graph made from Desmos
\begin{align} \mathrm{LHS} &:= \int_1^{1+x} \frac{\mathrm{d}t}{t} = \text{area under the curve} \\ \mathrm{RHS} &= x = \text{area of the rectangle} \end{align}
The curve $y = 1/x$ is below $y = 1$ on $x \ge 1$.
Exercise: complete this proof for the case $x \in (-1,0)$.
If you accept (otherwise this can easily be proved) that $\log ()$ is a concave function, then it suffices to show (cf. Jensen) that $x$ is a tangent to $\log(1+x)$. But this is obvious: $x$ and $\log(1+x)$ touch at $x=0$ and have the same slope ($1$) there.
