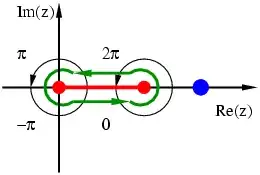
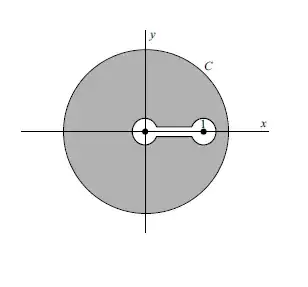
In a case like this, you have to contend with a residue at infinity. You can see this from the contour in your hint: as the radius of the circular contour $R \to \infty$, the integral about that contour approaches
$$i R \int_0^{2 \pi} d\phi \, \frac{e^{i \phi}}{\left(R^2 e^{i 2 \phi}-R^3 e^{i 3 \phi}\right)^{1/3}} \sim i 2 \pi (-1)^{-1/3}$$
However, you have to subtract out that dumbbell piece which excludes the branch points from the interior. This is where things get tricky. To this effect, we define
$$z^{-2/3} = e^{-(2/3) \log{z}}$$
such that $\arg{z} \in [-\pi,\pi)$. This definition is a result of the original branch cut of this factor being $(-\infty,0]$. The reaosn the branch is defined this way is because the argument of the log is negative real along the branch cut. Further define
$$(1-z)^{-1/3} = e^{-(1/3) \log{(1-z)}}$$
such that $\arg{(1-z)} \in [0,2\pi)$. This definition is a result of the original branch cut of this factor being $(-\infty,1]$. The reason the branch is defined like this is because, along the branch, $1-z$ is positive real along the branch cut.
To summarize, on the lines above and below the real axis, $z=x \in [0,1]$ and therefore $\arg{z} = 0$. On the line above the real axis, however, $\arg{(1-z)} = 2 \pi$. Therefore above the real axis, $z^{-2/3} (1-z)^{-1/3} = x^{-2/3} (1-x)^{-1/3} e^{-i 2 \pi/3}$ Below the real axis, $z^{-2/3} (1-z)^{-1/3} = x^{-2/3} (1-x)^{-1/3}$ because there, $\arg{(1-z)} = 0$.
Further, it should be clear that the integrals about the small circular arcs of radius $\epsilon$ around the branch points vanish as $\epsilon^{1/3}$.
Therefore, we may write
$$\left ( 1-e^{-i 2 \pi/3}\right) \int_0^1 dx \: x^{-2/3} (1-x)^{-1/3} = i 2 \pi (-1)^{-1/3}$$
Because that residue was calculated from the $1-z$ term, then $-1=e^{i \pi}$ and we have
$$\int_0^1 dx \: x^{-2/3} (1-x)^{-1/3} = i 2 \pi \frac{e^{-i \pi/3}}{1-e^{-i 2 \pi/3}} = \frac{\pi}{\sin{(\pi/3)}} = \frac{2 \pi}{\sqrt{3}}$$