Prove that $\frac{d}{dx}e^x=e^x$

Question

I would like to know how to prove that $$\frac{d}{dx}e^x=e^x$$ An argument I've seen used is that this is the defnition of the number $e$; we can say that for some number, let's call it $a$, the derivative of $a^x$ is $a^x$ and we've just called this number $e$. But a problem I have with this approach is that we are assuming that there exists a number $a$ that satisfies this property; how do we know it exists in the first place?

I've also seen an approach used that I think is very circular in its reasoning; they use the Maclaurin expansion of $e^x$ to prove by first principles that $\frac{d}{dx}e^x=e^x$. But the derivation of this series makes use of the very fact that $\frac{d}{dx}e^x=e^x$.

Any other proof will be very appreciated; an explanation of the $2$ above proofs would also be very useful.

Thank you for your help.

Answer 1

Define $e$ as $$e=\lim_{n\to\infty}\left(1+\frac1n\right)^n.$$ Thus $$e^x=\lim_{n\to\infty}\left(1+\frac1n\right)^{xn}.$$ Set $m=nx$ and note that $n\to\infty$ implies that $m\to\infty$, assuming $x$ is real. Then $$e^x=\lim_{m\to\infty}\left(1+\frac1{m/x}\right)^m=\lim_{m\to\infty}\left(1+\frac{x}{m}\right)^m.$$ Then $$\frac{d}{dx}e^x=\lim_{m\to\infty}\frac{d}{dx}\left(1+\frac{x}{m}\right)^m=\lim_{m\to\infty}\left(1+\frac{x}{m}\right)^{m-1}.$$ This is $$\frac{d}{dx}e^x=\lim_{m\to\infty}\frac{\left(1+\frac{x}{m}\right)^m}{1+x/m}=\frac{\lim_{m\to\infty}\left(1+\frac{x}{m}\right)^m}{\lim_{m\to\infty}(1+x/m)}=\frac{e^x}{1}=e^x.$$

---

A verification that $\frac{d}{dx}\lim=\lim\frac{d}{dx}$.

Let $C^1=C^1(\Bbb R)$ be the space of continuously differentiable functions $\Bbb R\to\Bbb R$. Similarly, let $C^0=C^0(\Bbb R)$ be the space of continuous functions $\Bbb R\to\Bbb R$. Then the differential operator map $D:C^1\to C^0$ given by $\phi(x)\mapsto \phi'(x)$ is a linear transformation.

To show this, note that for all $f,g\in C^1$ and $\alpha\in\Bbb R$, $$\begin{align} D(f+g)&=D(f)+D(g)\\ D(\alpha f)&=\alpha D(f). \end{align}$$ These are easy to check.

Since $D$ is a linear transformation it is continuous. That is, every convergent sequence of functions in $C^1$ is mapped by $D$ to a convergent sequence of functions in $C^0$: $$D\left(\lim_{n\to\infty}f_n\right)=\lim_{n\to\infty}D(f_n),$$ for a given convergent sequence of functions $(f_n)\subset C^1$. Clearly, $f_n(x)=(1+x/n)^n$ converges to $e^x$, so the above applies.

Answer 2

One nice approach is to define the function $\ln x$ (for $x\gt0$) as the integral

$$\ln x=\int_1^x{dt\over t}$$

and then show that this function has the property of a logarithm, namely $\ln(ab)=\ln a+\ln b$, after which one can define the function $\exp(x)$ to be the inverse of $\ln x$ and show it has the properties of an exponential, namely $\exp(x+y)=\exp(x)\cdot\exp(y)$. The number $e$ is defined as the (unique) value for which $\ln x=1$.

Answer 3

You can approach this from the limit definition of the derivative

$$ f'(x) = \lim_{h \to 0} \dfrac{f(x + h) - f(x)}{h}$$

With $f(x) = e^x$ this becomes

$$f'(x) = e^x \cdot \lim_{h \to 0} \dfrac{e^h - 1}{h}$$

and you can use your method of choice to show that

$$\lim_{h \to 0} \dfrac{e^h - 1}{h} = 1$$

To do this we'll use the limit definition of $e$: $$\displaystyle e = \lim_{n \to \infty} (1 + 1/n)^n$$

or equivalently

$$e = \lim_{x \to 0} (1 + x)^{1/x}$$

Introduce a change of variables, $t = e^h - 1$. Rewrite this as $\ln(t + 1) = h$.

$$\begin{align} \lim_{h \to 0} \dfrac{e^h - 1}{h} &= \lim_{t \to 0} \dfrac{t}{\ln(t+1)} \\ &=\lim_{t \to 0} \dfrac{1}{\frac{1}{t}\ln(t+1)} \\ &= \lim_{t \to 0} \dfrac{1}{\ln(t+1)^{1/t}} \\ &= \dfrac{1}{\ln(e)} \\ &= 1 \end{align}$$

Answer 4

One way to do this without making any assumptions is by starting with the definition of the natural logarithm, and working from there. This approach is outlined by Barry Cipra (+1). I posted an answer to How can we come up with the definition of natural logarithm?, which I will reproduce here. Although it seems unnatural to start with the logarithm and use it to define exponents, this approach is easy to make rigorous and can also be made fairly intuitive. As I mention in the post, the reason we might do choose to do this is because it is fairly difficult to define something like $2^\pi$. It's clear what $2^x$ would mean for positive integers, even for rational numbers, but not for irrational numbers. Starting with the logarithm, we can avoid this issue.

---

The study of the exponential function and the logarithm is motivated by the desire to find a way of modelling a particular kind of growth, where the rate of change of a quantity is proportional to the value of that quantity at any given time. Consider how the population of a colony of bacteria might change over time—perhaps it doubles every hour. Or how your wealth compounds when you put it into a bank. In both cases, we are dealing with exponential growth. Later, when Calculus makes rigorous the notion of 'instantaneous change', we may define an exponential function as a solution to the differential equation $$ \frac{dy}{dx}=ky \, . $$ Solving this equation, we find that $$ kx+C = \int \frac{1}{y} \, dy \, . \tag{*}\label{*} $$ It seems like we have hit a roadblock, since we cannot integrate $1/y$ using the rule $$ \int y^n \, dy = \frac{y^{n+1}}{n+1}+C \, , $$ since that would lead to division by zero. However, the fundamental theorem of calculus tells us that the set of antiderivatives of $1/y$ must be $$ \int_{a}^{y} \frac{1}{t} \, dt \, . $$ This is a set of functions that differ by a constant as we vary the value of $a$. However, since there is already a constant on the LHS of $\eqref{*}$, we can assume that $a=1$ without loss of generality. This yields $$ kx+C = \int_{1}^{y} \frac{1}{t} \, dt \, . $$ Let $f(y)=\int_{1}^{y} \frac{1}{t} \, dt$. This function represents the area of the region bounded by the hyperbola $1/t$, the horizontal axis, and the vertical lines $t=1$ and $t=y$:

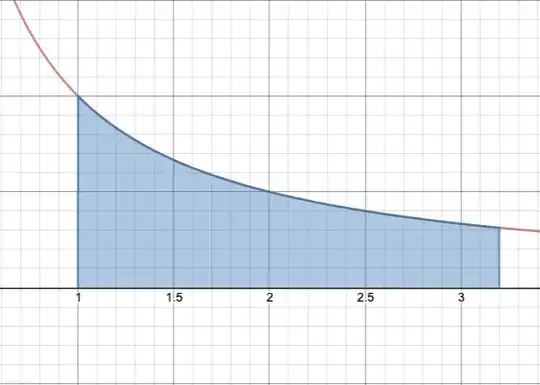
As the value of $y$ gets larger, the area of this region also gets larger. We can then verify that $f$ is strictly increasing, meaning that $f^{-1}$ exists. Hence, $$ kx+C = f(y) \implies y = f^{-1}(kx+C) \, . $$ Since growth of this kind is called exponential growth, it only seems right to bestow upon the function $f^{-1}$ the new name $\exp$. The statement reads more nicely as $$ y=\exp(kx+C) \, . $$ Of all of the types of exponential growth, the most pleasing is that in which the rate of change of a quantity is equal to the value of that quantity (not just proportional to it). Since the set of solutions to $dy/dx = ky$ is $y=\exp(kx+C)$, the set of solutions to $dy/dx = y$ is $$ y=\exp(x+C) \, . $$ And of these solutions, you will no doubt agree that the simplest and most aesthetic is $$ y=\exp(x) \, , $$ where $\exp(x)$ is defined as the inverse of $f(x)=\int_{1}^{x} \frac{1}{t} \, dt$. For obvious reasons, this function is called the natural exponentional function. There seems to be clear parallels between $\exp$ and functions of the form $g(x)=a^x$. If we return to our examples of exponential modelling—the colony of bacteria that doubles in size every hour—it certainly seems that $2^x$ is an exponential function. After all, the growth of a bacterial colony is proportional to its population at any given point in time. This suggests that $$ 2^x = \exp(kx+C) $$ for some values of $k$ and $C$. (So far, we haven't actually defined what $2^x$ means when $x$ equals $\sqrt{2}$, say, but we'll leave to the side for the moment, and use an 'intuitive' definition of irrational exponents, where $2^{\sqrt{2}} \approx 2^{1.41421}$.) Suspecting that $a^x$ and $\exp(x)$ are somehow linked, we try to recall the essential properties of $a^x$, hoping that $\exp(x)$ shares these properties. The most important of these properties is that $$ a^x \cdot a^y = a^{x+y} \, . $$ And it turns out that $\exp(x)$ also has this property! In other words, $$ \exp(p) \cdot \exp(q) = \exp(p+q) \, . $$ However, proving this takes a little work. Since $\exp(x)$ is defined as the inverse of $f(x)=\int_{1}^{x}\frac{1}{t} \, dt$, it seems sensible to use this integral in our proof. Showing that $\exp(p) \cdot \exp(q) = \exp(p+q)$ is actually equivalent to showing that $f(r) + f(s) = f(rs)$, since \begin{align} &f(r) + f(s) = f(rs) \\ \iff &f^{-1}(f(r)+f(s)) = rs \\ \iff &f^{-1}(f(r)+f(s)) = f^{-1}(f(r)) \cdot f^{-1}(f(s)) \\ \iff &\exp(p+q) = \exp(p) \cdot \exp(q) \end{align} (And this should make intuitive sense, too. Notice how $f$ changes multiplication into addition, and so it is only natural that $f^{-1}$ changes addition into multiplication.) There is also a slick way to prove that $f(r)+f(s)=f(rs)$: $$ \int_{1}^{rs}\frac{1}{t} \, dt = \int_{1}^{r}\frac{1}{t} \, dt + \int_{r}^{rs}\frac{1}{t} \, dt $$ Let $z=t/r$, meaning that $dz=\frac{1}{r}dt=\frac{z}{t}dt$. Then we have \begin{align} \int_{1}^{rs}\frac{1}{t} \, dt &= \int_{1}^{r}\frac{1}{t} \, dt + \int_{1}^{s}\frac{1}{z} \, dz \\ f(rs) &= f(r) + f(s) \, . \end{align} Now that we have established that $\exp(p) \cdot \exp(q)=\exp(p+q)$, it seems reasonable to conjecture that $\exp(x)$ is actually equal to $a^x$ for some base $a$. To find that base, we plug in $x=1$, yielding $\exp(1)$, which we will abbreviate as $e$. This means that $$ e^x = \exp(x) \, . $$ This notation, apart from being very convenient, is also entirely valid. To reiterate, $\exp(p) \cdot \exp(q)=\exp(p+q)$, and so $$ e^p \cdot e^q = e^{p+q} $$ as expected. Geometrically, $e$ represents the number $a$ for which $\int_{1}^{a}\frac{1}{t} \, dt = 1$. This property follows directly if one recalls the definition of $\exp$. And since $\log_a(x)$ is defined as the inverse of $a^x$, it is evident that $\log_e(x)$ is the inverse of $e^x$. But we know that the inverse of $\exp(x)$ is $f(x)=\int_{1}^{x}\frac{1}{t} \, dt$, and putting these statements together, we find that $$ \log_{e}(x) = \int_{1}^{x}\frac{1}{t} \, dt \, . $$ In fact, this logarithm is so important, so natural, that we often dispense with the base $e$ entirely and write $$ \log(x) = \int_{1}^{x}\frac{1}{t} \, dt \, . $$ Earlier, we mentioned the difficulty of defining $a^x$ when $x$ is an irrational number. The logarithm solves this problem. For rational $x$, we know that $$ a^x = e^{x\log(a)} \, . $$ But the RHS makes sense for all $x$, and so we may define $$ a^x = e^{x\log(a)} \, , $$ for $a>0$. And defining exponents in this way means that $$ a^x \cdot a^y = a^{x+y} \, , $$ still holds even for irrational exponents! The proof of this fact follows smoothly if we unravel the definition of $a^x$: $$ a^x = e^{x\log(a)} = \exp(x\log(a)) \, , $$ where $\exp(x)=\log^{-1}(x)$ and $\log(x) = \int_{1}^{x}\frac{1}{t} \, dt$. Armed with this knowledge, we return to the differential equation we were trying to solve earlier, and finally obtain the solution we were expecting. \begin{align} \frac{dy}{dx} &= ky \\ \int k \, dx &= \int\frac{1}{y} \, dy \\ kx + C &= \log(y) \\ y&=e^{kx+C} = e^{kx} \cdot e^{C} = Ae^{kx} \text{ where $A=e^C$} \end{align} Since $a^x$ simply represents $e$ being raised to another base, functions such as $2^x$ are also included in the solution set. In particular, $$ \frac{d}{dx}(a^x) = \frac{d}{dx}(e^{x\log(a)}) = e^{x\log(a)} \cdot \log(a) = a^x \cdot \log(a) \, , $$ and so $k=\log(a)$. Note that the derivative of $e^x$ is simply a special case of this where $\log(e)=1$. Hopefully, this should provide the motivation behind defining the logarithm as $\int_{1}^{x}\frac{1}{t} \, dt$.

---

There is another way of understanding why functions of the form $f(x)=a^x$ grow in the way they do. If we differentiate $a^x$ with respect to $x$ from first principles, we get \begin{align} \lim_{\Delta x \to 0}\frac{a^{x+\Delta x}-a^x}{\Delta x} &= a^x \cdot \lim_{\Delta x \to 0}\frac{a^{\Delta x} - 1}{\Delta x} \\ &= a^x \cdot f'(0) \, . \end{align} In other words, the growth rate is proportional to the value of $a^x$ at any given point, with the gradient at $x=0$ being the proportionality constant. The natural logarithm comes in handy here: $$ f'(0) = \lim_{\Delta x \to 0}\frac{a^{\Delta x} - 1}{\Delta x} \, . $$ Exercise: prove that this limit is equal to $\log(a)$. This is tricky if you want to avoid using L'Hôpital's rule.

Answer 5

This is based on the definition

$$e = \lim_{n \to \infty} \left(1+\frac1n\right)^n$$

and the definition of $\ln$ as inverse of $e^x$.

Let $y=e^x$, then

$$\begin{align*} x &= \ln y\\ \frac{dx}{dy} &= \lim_{h\to0}\frac{\ln(y+h)-\ln y}{h}\\ &=\lim_{h\to0}\ln\left(1+\frac{h}{y}\right)^\frac1h\\ &=\ln\lim_{h\to0}\left(1+\frac{h}{y}\right)^{\frac yh\cdot \frac1y}\\ &= \ln \left(e^\frac1y\right)\\ &= \frac1y\\ &= \frac1{e^x}\\ \frac{dy}{dx} &= e^x \end{align*}$$

Answer 6

Suppose we've already proved that $\frac{d}{dx} a^x = g(a) a^x$ for some function $g : \mathbb{R}_{> 0} \to \mathbb{R}$ (see this post for example). The question is then "Does there exist $a \in \mathbb{R}_{>0}$ such that $g(a) = 1$ ?"

Observe that, by the chain rule, for any $k \in \mathbb{R}$: $$ \frac{d}{dx} a^{kx} = k g(a) a^{kx} $$ On the other hand $$ \frac{d}{dx} a^{kx} = \frac{d}{dx} (a^k)^x = g(a^k) (a^k)^x = g(a^k) a^{kx} $$ Thus $kg(a) = g(a^k)$ for all $a \in \mathbb{R}_{>0}$ and $k \in \mathbb{R}$.

In particular, we may set $k = \frac{1}{g(a)}$ for some $a \in \mathbb{R}$ such that $g(a) \neq 0$ (if $g = 0$, then all exponential functions are constant, which we know is not true). Then $$ \frac{d}{dx} (a^k)^x = g(a^k) (a^k)^x = kg(a) (a^k)^x = (a^k)^x $$ Therefore, if $g(a) \neq 0$, $e \equiv a^{\frac{1}{g(a)}}$ is a number such that $$ \frac{d}{dx} e^x = e^x $$ By carrying the analysis further, we could convince ourselves that $a^{\frac{1}{g(a)}}$ is a unique number, i.e. does not depend on $a$.

Answer 7

Let $y=e^x$.

Taking $\text{ln}$ both sides, we obtain

$\text{ln}y=x\text{ln}e=x$.

Differentiating w.r.t. $x$, we have

$$\frac{1}{y}\frac{dy}{dx}=1$$ $$\frac{dy}{dx}=y$$ $$\frac{d}{dx}e^x=e^x.$$

Answer 8

Comment:

$y=e^x$

Due to definition of derivative we can write:

$$y'=\lim_{\Delta x\rightarrow 0}\frac{e^{x+\Delta x}-e^x}{\Delta x}=\lim_{\Delta x\rightarrow 0}e^x(\frac {e^{\Delta x}-1}{\Delta x})=e^x$$

Provided we prove that:

$\lim_{\Delta x\rightarrow 0} \frac {e^{\Delta x}-1}{\Delta x}=1$

Answer 9

The first time we are acquainted with exponentiation is with the idea of it as repeated multiplication. For $n \in \mathbb{N}$, we may define $$ a^n=\underbrace{a \cdot a \cdot a \cdot \ldots \cdot a}_{\text{$n$ times}} \, . $$ This helps us establish an important principle about exponentiation, $$ a^{x+y}=a^x \cdot a^y \, , $$ which will guide us in how we define $a^n$ when $n\not\in\mathbb{N}$. To begin with, $a^0$ should be equal to $1$, since $$ a^0\cdot a^n=a^n \implies a^0=\frac{a^n}{a^n}=1 \, . $$ For the same reason, $a^{-n}$ should be equal to $1/a^n$. If $n$ is a rational number $p/q$, then $$ a^n=(\sqrt[q]{a})^p \, . $$ It's worth noting at this point that this definiton does not apply when the base $a$ is a negative number, since $(-5)^{1/2}$ is meaningless within the context of real numbers. It is possible to partially extend the definition, so that $a^{p/q}$ is meaningful when $q$ is an odd number, but from here on in we will only define $a^n$ for when $a\geq0$.* We are still unsure about how to define $a^n$ for $n\in\mathbb{R}$, since $n$ could be an irrational number. Nevertheless, it seems natural that $a^{\sqrt{2}}$ should be approximately equal to $a^{1.41421}$, and this motivatives the below definition for irrational exponents: $$ a^n=\lim_{m(\in\mathbb{Q})\to n} a^m \, . $$

---

Now that we have formally defined $a^x$ for $a\geq0$, $x\in\mathbb{R}$, we can begin to examine its properties. You will no doubt be familiar with the phrase 'exponential growth'—growth in which the rate of change of a quantity is proportional to the quantity at any given time. This means that an exponentional function may be characteristed as any solution to $$ y'(x) = cy(x) $$ for some constant $c$. The term 'exponentional' can give us a clue as to which functions exhibit this property, namely the ones we have just studied! If $y(x)=a^x$, then \begin{align} \frac{dy}{dx} &= \lim_{\Delta x \to 0}\frac{a^{x+\Delta x}-a^x}{\Delta x} \\ &= a^x \lim_{\Delta x \to 0}\frac{a^{\Delta x}-1}{\Delta x} \end{align} Note that the final limit is simply $y'(0)$, meaning that $y'(x)$ does indeed equal $cy(x)$, with $c$ being equal to the slope of $a^x$ at the point $(0,1)$. This helps explain one of the classic definitions of the constant $e$: it is the unique number $a$ such that $$ \lim_{\Delta x \to 0}\frac{a^{\Delta x}-1}{\Delta x} = 1 \, . $$ This means that $e^x$ is its own derivative. This approach has two deficiencies, though:

• We haven't proven that the limit $$\lim_{\Delta x \to 0}\frac{a^{\Delta x}-1}{\Delta x}$$ exists.
• We haven't shown that there is such a number where the above limit is equal to $1$.

This can be remedied by appealing to one of the alternative definitions of $e$.