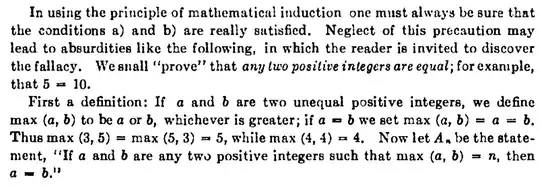2

I've been reading Courant/Robbins' "What is Mathematics?"

The first time they mentions $a),b)$ is here:

enter image description here

In another section of the book, he points out there is an alternative formulation:

enter image description here

Now here:

enter image description here enter image description here

I don't see what is the fallacy here: He showed that $A_1$ is true, that is: He showed that $b)$ is true. But when trying to show that $a)$ is true, it seems he did a weird thing in there that looks like $a)$ but isn't? It's not clear to me. Can you help?

Red Banana
  • 23,956
  • 20
  • 91
  • 192
  • 1
    The argument in part (a) is invalid. Consider $r=1$, with $a=2, b=1$. Then $\alpha = 2 - 1 = 1$ and $\beta = 1 - 1 = 0$. Zero is not a positive integer, so you can't apply $A_1$ to $\alpha$ and $\beta$. –  Dec 04 '20 at 23:03
  • 2
    Not a duplicate, but related. If you're unsure why an inductive step fails, work through the first example of it. – J.G. Dec 04 '20 at 23:10

3 Answers3

4

There is nothing weird about what he’s doing in (a): he is simply trying to apply the induction hypothesis. The induction hypothesis is that $A_r$ is true: if $\max(a,b)=r$, then $a=b$. Now we assume that $a$ and $b$ are positive integers such that $\max(a,b)=r+1$. Then $\max(a-1,b-1)=r$, so by the induction hypothesis $a-1=b-1$, and therefore $a=b$.

The problem with this is that $A_r$ is the statement that if $a$ and $b$ are any two positive integers, and $\max(a,b)=r$, then $a=b$, and the fact that $a$ and $b$ are positive does not ensure that $a-1$ and $b-1$ are positive. If at least one of $a$ and $b$ is equal to $1$, we cannot apply the induction hypothesis $A_r$ to $a-1$ and $b-1$, because they are not both positive integers.

Brian M. Scott
  • 616,228
  • Then it's something subtle. I was expecting him to not apply some of the conditions in a more obvious way, I guess. – Red Banana Dec 05 '20 at 01:36
4

It is obvious that $A_2$ is false. (The maximum being two doesn’t imply the two positive integers are equal.) Thus the argument in the induction step in part (a) must be invalid.

Where is the error? It’s in the tacit assumption that the maximum of $\alpha$ and $\beta$ is even defined (according to the precise definition given in the statement of the problem). The trouble is that it might not be: indeed it won’t be if $a$ or $b$ is equal to one, for then either $\alpha$ or $\beta$ is not positive. The maximum function, as defined in the problem, is defined only for positive integers.

symplectomorphic
  • 18,604
  • +1 Good point: Applying max beyond its definition is the first error to appear in the argument. On the other hand, if that were the only error, it wouldn't be fatal. – Chris Culter Dec 04 '20 at 23:25
  • 1
    Well, it’s fatal as written, but I know what you mean. (My point is that all we must do to diagnose the formal invalidity is say that it is invalid to write $\max(\alpha, \beta)=r$.) – symplectomorphic Dec 04 '20 at 23:26
3

$\alpha$ and $\beta$ don't necessarily satisfy the hypotheses of $A_r$.

Chris Culter
  • 26,806