2

We randomly take $51$ numbers from 159 natural numbers $1,...,159$ without replacement. Let $\alpha$ be a random variable equal to the sum of the selected numbers. Find the variance of $\alpha$.

Firstly I need to understand something about $\alpha$ destribution. There are totally $$C^{51}_{159} = \frac{159!}{51!108!}$$ kinds of sums. A lot of them are equal, because $$\sum_{i=1}^{51}i = 1326\leq\alpha\leq\sum_{i=109}^{159}i=6834$$ Consequenlty, I want to know how many subsets of $51$ numbers have the sum equal to $N$, where $1362\leq N\leq6834$. I'm stuck here because I don't know how to do it.

Adam Rubinson
  • 20,052
Sneach hcaens
  • 372
  • 1
    I'm not sure the combinatorial approach is going to lead you to a solution. Consider integers 1 through 159 as a population. Find its variance. What would be the variance of the sum of $n=51$ observations with replacement from that population? See end of my extended comment with simulation. – BruceET Nov 30 '20 at 10:37
  • "I want to know how many subsets of $51$ numbers have the sum equal to $N."\ $ So, given $N \in \ ${$1326,...,6834$}, you want to find the number of solutions to the Diophantine equation: $n_1 + n_2 + ... + n_{51} = N;\ n_k \in$ {$1, 2, ..., 51$} for each $k \in$ {$1, 2, ..., 51$} and $n_i \neq n_j$ if $i \neq j$. I think this is a well-known combinatorics problem with an "easy" solution, but I only came across the problem in passing on this site and can't remember the solution or what the question title was. But I'm fairly certain if you search for it you'll find an answer on this site. – Adam Rubinson Dec 01 '20 at 14:18
  • @AdamRubinson I don't recall any easy solution, as the variables $n_i$ are constrained (with an upperbound and also distinct)... Or maybe I just haven't heard of it :) – Gareth Ma Dec 01 '20 at 14:20
  • Maybe not an easy solution, but I'm sure there is a way to do it. What about: https://math.stackexchange.com/questions/3286112/variance-of-sum-of-k-randomly-drawn-numbers-from-1-n?rq=1 or: https://math.stackexchange.com/questions/2813390/if-m-tickets-are-drawn-out-of-n-tickets-numbered-1-to-n-find-variance-o – Adam Rubinson Dec 01 '20 at 14:21
  • @AdamRubinson Wow. The theorectical variance is 73440 which matches the numerical data too. – Gareth Ma Dec 01 '20 at 14:23
  • @Gareth - Please remind me how to hyperlink in a comment. – Adam Rubinson Dec 01 '20 at 14:26
  • @AdamRubinson Not sure, I pressed "flag" then by duplicate and it auto-generates the comment above :) – Gareth Ma Dec 01 '20 at 14:26
  • Ah, if only I had waited a few more minutes before I started typing my solution... – Neat Math Dec 01 '20 at 15:06
  • @GarethMa Where's the "flag"? I don't see any. I just do text but obviously your way is better. – Neat Math Dec 01 '20 at 15:08
  • Guys, but why These random variables $X_i$ are independent? I think it is whrong. Because if we take ball on $i-th step$ there are $n - i$ balls in urn. @GarethMa – Sneach hcaens Dec 01 '20 at 16:59
  • @Sneachhcaens No they are not but by symmetry you can compute the first and second moments easily. – Neat Math Dec 01 '20 at 17:33
  • It is very strange that $\alpha\leq 6834$ has so great dispercion. @NeatMath – Sneach hcaens Dec 01 '20 at 17:40
  • @Sneachhcaens Check here. I didn't have time to simplify the final expression earlier today but look for "sanity checks" in the first answer in the link. It makes sense to me. – Neat Math Dec 01 '20 at 17:57

2 Answers2

4

Replace 51 and 159 with $n, M$ respectively. We have a vector $\mathbf{x}_{n\times 1}$ which follows a multivariate distribution, and $\alpha = \sum_{i=1}^n x_i$ where $x_i$ is the $i^{th}$ component of $\mathbf x$.

Then, by symmetry, $E(\alpha)=E(\sum x_i)=\sum_i E(x_i) =nE(x_1)= \frac{n(M+1)}{2}$.

$$E(\alpha^2)=E\left(\sum_i x_i\right)^2 = E\left(\sum_i x_i^2\right)+E\left(\sum_{i\neq j} x_i x_j \right)$$

Again by symmetry $$ E\left(\sum_i x_i^2\right)=nE(x_1^2)=\frac 16 n(M+1)(2M+1) $$

$$ E\left(\sum_{i\neq j} x_i x_j \right)=(n^2-n)E(x_1 x_2)=\frac{n^2-n}{M^2-M}\sum_{i\ne j}ij = \frac{n^2-n}{M^2-M}\left(\left(\frac{M(M+1)}{2}\right)^2 - \frac{M(M+1)(2M+1)}{6}\right) \\= \frac{1}{12} (n^2-n)(M+1)(3M+2) $$

Therefore $$\text{var } \alpha = E(\alpha^2) - (E(\alpha))^2 = \cdots = 73440$$

Neat Math
  • 4,790
1

Comment: You can get a reasonable approximation to $Var(\alpha)$ by simulation. In the simulation, I assume the 51 numbers are selected without replacement.

set.seed(2020)
alpha = replicate(10^5, sum(sample(1:159, 51)))
summary(alpha)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   2915    3897    4081    4081    4266    5275

Notice that among the 100,000 samples I summed, all of the totals are between the two numbers you mention in your question.

var(alpha)
[1] 74069.39
sd(alpha)
[1] 272.1569

A histogram of the simulated values of $\alpha$ looks approximately normal, so I show the best-fitting normal density along wit the histogram.

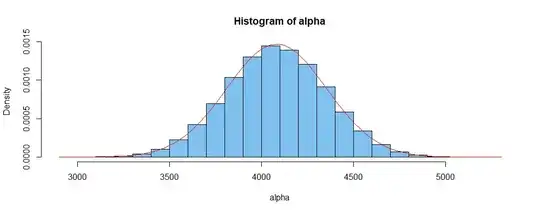
enter image description here

hist(alpha, prob=T, col="skyblue2")
 curve(dnorm(x, mean(alpha), sd(alpha)), add=T, col="red")

With replacement, the variance is somewhat larger. (Again here the distribution of $\alpha$ seems approximately normal; histogram not shown.)

set.seed(1130)
alpha = replicate(10^6, sum(sample(1:159, 51, rep=T)))
summary(alpha)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   2593    3859    4080    4080    4302    5590 
var(alpha)
[1] 107274.7

Possible solution: If you consider the population to be numbers 1 through 159, then the population has variance 2120, and the sum of a random sample with replacement should have variance 51 times as large, which is 108,120, which seems to agree with the simulated result within the margin of simulation error.

var(1:159)
[1] 2120
51*var(1:159)
[1] 108120
BruceET
  • 51,500