I would like to find inverse Laplace transform of the function: $$F(s)=e^{-a\sqrt{s(s+b)}}$$ which $a$ and $b$ are positive real numbers and $s$ is a complex variable. It would be appreciated if someone can help me.
1 Answers
See my solution to this problem. The analysis is identical, save for the denominator.
$$\oint_C ds \,e^{-a \sqrt{s (s+b)}}\, e^{s t}$$
where $C$ is the following contour pictured below:
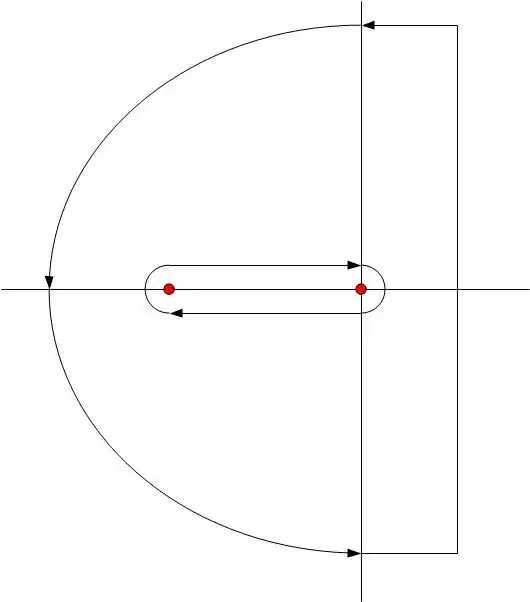
This one's a bit odd because we are removing the branch point singularities by subtracting the inner contour $C_i$ from the outer contour $C_o$, i.e. $C=C_o+C_i$.
The integral about $C$ consists of the integral about vertical path (that ultimately becomes the ILT) and the integral about the outer arc. We expect that this latter integral vanishes as the radius of the arc gets larger; this only happens when $a \lt t$ as shown below, by letting $s=R e^{i \phi}$; this integral over this arc is, for large $R$:
$$\left| \int_{\pi/2}^{3 \pi/2} d\phi \,e^{R (t-a) \cos{\phi}} \right|$$
Note that $\cos{\phi} \lt 0$ over the integration region, so that the integral only vanishes for $a \lt t$ when the contour opens to the left.
This leaves the integral over $C_i$ which consists of integrals above and below the real axis, between the branch points, and integrals about small circular arcs about the branch points. These latter integrals vanish in the limit of the radii of the arcs going to zero. Thus, we are left with
$$\int_{c-i \infty}^{c+i \infty} ds e^{-a \sqrt{s (s+b)}}\, e^{s t} - \underbrace{ \int_0^{b} dx\, e^{i a \sqrt{x (b-x)}}\, e^{-x t}}_{s=e^{-i \pi} x} + \underbrace{ \int_0^{b} dx\, e^{-i a \sqrt{x (b-x)}}\, e^{-x t}}_{s=e^{i \pi} x} = 0$$
We set the sum of the integrals to zero because of Cauchy's theorem, i.e., there are no poles inside the contour $C$. The second integral is the integral over the line below the real axis; the third is the integral over the line above the real axis. Note that the phase transition was continuous from $-\pi$ to $\pi$ because we did not cross the branch cut; we did not see this explicitly because that information was included in the integrals about the branch points which vanished.
We do a little algebra and we have a real-valued integral for the ILT:
$$\frac{1}{i 2 \pi} \int_{c-i \infty}^{c+i \infty} ds \, e^{-a \sqrt{s (s+b)}} e^{s t} = \frac{1}{\pi} \int_0^b dx \, \sin{\left [ a \sqrt{x (b-x)}\right]} e^{-x t}$$
We make similar substitutions as with the other solution and we find the RHS is equal to
$$\begin{align}\frac{b}{2 \pi} e^{- b t/2} \int_0^{\pi} d\phi \, \sin{\phi} \, \sin{\left[\frac12 a b \sin{\phi}\right]} \, e^{b t/2 \cos{\phi}}\\ = -e^{-b t/2} \frac{1}{\pi} \frac{\partial}{\partial a} \int_0^{\pi} d\phi \, \cos{\left[\frac12 a b \sin{\phi}\right]} \, e^{b t/2 \cos{\phi}}\\ = -e^{-b t/2} \frac{\partial}{\partial a} I_0\left( \frac{b}{2} \sqrt{t^2-a^2}\right)\end{align}$$
Note again that the contour is only closed to the left when $t>a$; when $t<a$ it is closed to the right. Therefore the ILT of $e^{-a \sqrt{s (s+b)}}$ is
$$\frac{a b}{2} e^{-b t/2} \left(t^2-a^2\right)^{-1/2} \, I_1\left(\frac{b}{2}\sqrt{t^2-a^2}\right) H(t-a)$$
- 138,521
-
What software do you typically use to draw? And of-course +1. – May 15 '13 at 04:28
-
@user17762: (Can I call you Marvis?) I use Microsoft Visio, only because I use it a lot for my work. – Ron Gordon May 15 '13 at 04:29
-
Cool. Thanks. I would prefer user17762. But either way is fine. – May 15 '13 at 04:30
-
@user17762: whatever you prefer. – Ron Gordon May 15 '13 at 04:30
-
First thank you for your solution. I think the following relation is correct. $$\frac{b}{2 \pi} e^{- b t/2} \int_0^{\pi} d\phi , \sin{\phi} , \cos{\left[\frac12 a b \sin{\phi}\right]} , e^{b t/2 \cos{\phi}}\ = -e^{-b t/2} \frac{1}{\pi} \frac{\partial}{\partial a} \int_0^{\pi} d\phi , \sin{\left[\frac12 a b \sin{\phi}\right]} , e^{b t/2 \cos{\phi}}$$ I mean $sin$ instead of $cos$. Am I right? If yes, how does this will affect to the final solution? Thanks again – Vahid May 15 '13 at 12:53
-
1@vahid: you caught a major error! There was no factor of $i$ in the contour integrals above, so I should have had a sine and not a cosine in the integral. It now all works out - the answer must be the derivative of the previous result with respect to $a$. Thank you. – Ron Gordon May 15 '13 at 14:31
-
Thank you very much Ron. The comment is very useful for me. – Vahid May 16 '13 at 01:43