It would be appreciate if someone help me to obtain the inverse Laplace transformation of the complex function $F(s)=\frac{e^{-\frac lc\sqrt {s(s+r_0)}}}{\frac lc\sqrt {s(s+r_0)}}$ where $r_0,l,c$ are positive real and $s$ is a complex variable. Thanks
1 Answers
This one is interesting because of the presence of two branch points: one at $s=0$ and the other at $s=-r_0$. We will consider the complex integral
$$\oint_C ds \frac{e^{-a \sqrt{s (s+r_0)}}}{\sqrt{s (s+r_0)}} e^{s t}$$
where $C$ is the following contour pictured below:
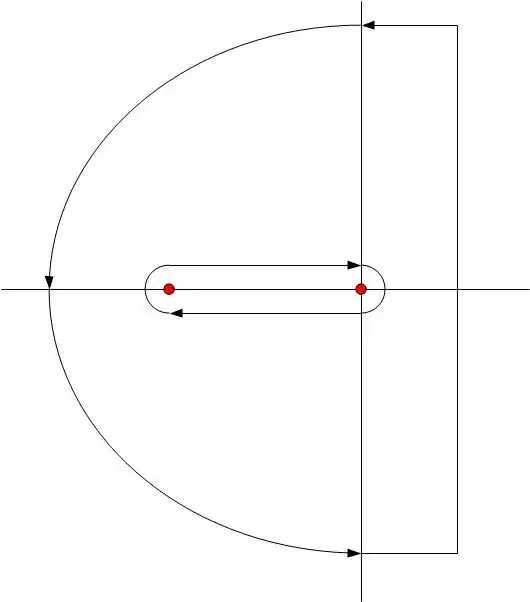
This one's a bit odd because we are removing the branch point singularities by subtracting the inner contour $C_i$ from the outer contour $C_o$, i.e. $C=C_o+C_i$.
The integral about $C$ consists of the integral about vertical path (that ultimately becomes the ILT) and the integral about the outer arc. We expect that this latter integral vanishes as the radius of the arc gets larger; this only happens when $a \lt t$ as shown below, by letting $s=R e^{i \phi}$; this integral over this arc is, for large $R$:
$$\left| \int_{\pi/2}^{3 \pi/2} d\phi \,e^{R (t-a) \cos{\phi}} \right|$$
Note that $\cos{\phi} \lt 0$ over the integration region, so that the integral only vanishes for $a \lt t$ when the contour opens to the left.
This leaves the integral over $C_i$ which consists of integrals above and below the real axis, between the branch points, and integrals about small circular arcs about the branch points. These latter integrals vanish in the limit of the radii of the arcs going to zero. Thus, we are left with
$$\int_{c-i \infty}^{c+i \infty} ds \frac{e^{-a \sqrt{s (s+r_0)}}}{\sqrt{s (s+r_0)}} e^{s t} - \underbrace{i \int_0^{r_0} dx \frac{e^{i a \sqrt{x (r_0-x)}}}{\sqrt{x (r_0-x)}} e^{-x t}}_{s=e^{-i \pi} x} - \underbrace{i \int_0^{r_0} dx \frac{e^{-i a \sqrt{x (r_0-x)}}}{\sqrt{x (r_0-x)}} e^{-x t}}_{s=e^{i \pi} x} = 0$$
We set the sum of the integrals to zero because of Cauchy's theorem, i.e., there are no poles inside the contour $C$. The second integral is the integral over the line below the real axis; the third is the integral over the line above the real axis. Note that the phase transition was continuous from $-\pi$ to $\pi$ because we did not cross the branch cut; we did not see this explicitly because that information was included in the integrals about the branch points which vanished.
We do a little algebra and we have a real-valued integral for the ILT:
$$\frac{1}{i 2 \pi} \int_{c-i \infty}^{c+i \infty} ds \frac{e^{-a \sqrt{s (s+r_0)}}}{\sqrt{s (s+r_0)}} e^{s t} = \frac{1}{\pi} \int_0^{r_0} dx \frac{\cos{\left[ a \sqrt{x (r_0-x)}\right]}}{\sqrt{x (r_0-x)}} e^{-x t}$$
Using a substitution of $x=u^2$ and performing a series of trig substitutions (which I leave to the reader), I get for the integral
$$\frac{1}{\pi} e^{-r_0 t/2} \int_0^{\pi} d\theta \: \cos{\left(\frac{1}{2} a r_0 \sin{\theta}\right)} e^{(r_0 t/2) \cos{\theta}}$$
To evaluate, use the fact that
$$\cos{(b \sin{\theta})} = J_0(b) + 2 \sum_{k=1}^{\infty} J_{2 k}(b) \cos{2 k \theta}$$
and
$$\int_0^{\pi} d\theta \: \cos{n \theta} \, e^{z \cos{\theta}} = \pi I_n(z)$$
where $J_n$ is the $n$th Bessel of the first kind, and $I_n$ is the $n$th modified Bessel of the first kind.
We thus have a result for $t \gt a$. When $a \ge t$, however, we choose the integration contour to open to the right rather than the left. Because there are no poles or branch points there, the ILT for $a \ge t$ is zero.
The result is
$$\frac{1}{i 2 \pi} \int_{c-i \infty}^{c+i \infty} ds \frac{e^{-a \sqrt{s (s+r_0)}}}{\sqrt{s (s+r_0)}} e^{s t} = e^{-r_0 t/2} H(t-a) \left [ J_0\left(\frac{1}{2} a r_0\right) I_0\left(\frac{1}{2} r_0 t\right) \\+ 2 \sum_{k=1}^{\infty} J_{2 k}\left(\frac{1}{2} a r_0\right) I_{2 k}\left(\frac{1}{2} r_0 t\right)\right ] $$
where $H$ is the Heaviside step function:
$$H(x) = \begin{cases} \\ 1 & x > 0\\ 0 & x < 0\end{cases}$$
ADDENDUM
The answer simplifies ridiculously; see here. I get
$$f(t) = H(t-a) I_0\left(\frac{1}{2} r_0 \sqrt{t^2-a^2}\right) e^{-r_0 t/2} $$
- 138,521
-
Have I seen a comment from you including the word Disneyworld, or did I dream? I can't find it anymore: it disappeared before I could reply. Anyway, thanks, Ron. And +1, of course. – Julien Apr 23 '13 at 01:42
-
@julien: yeah, something to do with the 20k club. Not sure why it would have disappeared, though. Anyway, congrats again. – Ron Gordon Apr 23 '13 at 05:38
-
Can you explain why you can use regular residue theorem for interior domains when there are non-isolated singularities inside of both contours? – Random Variable Apr 23 '13 at 16:10
-
@RandomVariable: I am not using the Residue theorem, but Cauchy's Theorem, as there are no isolated poles. That said, I do not know what you mean by "non-isolated singularities." – Ron Gordon Apr 23 '13 at 16:12
-
Branch points are non-isolated singularities. So the function is not analytic (or even meromorphic) inside of the contour. Why does Cauchy's theorem even apply? – Random Variable Apr 23 '13 at 16:24
-
2@RandomVariable: the point of the inner contour is to subtract it out from the outer contour. We still have a connected region and, yes, the function is indeed analytic inside the (net) contour; that is, inside the outer contour, outside the inner contour. Note the direction in which the inner contour is taken (clockwise) versus the outer contour (counter-clockwise). – Ron Gordon Apr 23 '13 at 16:26
-
If I was forced to do this problem, I would use a left-facing keyhole contour with half-circle indentations above and below $z=-r_{0}$. – Random Variable Apr 23 '13 at 17:21
-
2I tried that, but I was a bit worried about the branch point $s=0$. That's why I did it the way I did. – Ron Gordon Apr 23 '13 at 17:43
-
1My understanding of what you did is the following: The integrand $f(s)$ is analytic outside and on $C_{i}$. So if you integrate $f(s)$ around $C_{i}$ clockwise, it's equal to $2 \pi i \text{Res}[f(s),\infty]$. But $ 2 \pi i \text{Res}[f,\infty] = \int_{c-i \infty}^{c+i \infty} ds \frac{e^{-a \sqrt{s (s+r_0)}}}{\sqrt{s (s+r_0)}} e^{s t}$. – Random Variable Apr 23 '13 at 18:21
-
@RandomVariable: no, not quite. The crux is that the integral over the contour (the outer contour and the inner contour, in their respective directions) is zero. The integral over the vertical piece is the ILT; the rest is what we end up actually using. – Ron Gordon Apr 23 '13 at 18:23
-
@RandomVariable: you are not bothering me, I enjoy this. Residue at $\infty$. Hmmm...you're gonna have to help me. And forgive me: I'm just a knucklehead physicist with a rather utilitarian view of math in general. Please explain what a residue at infinity buys us. – Ron Gordon Apr 23 '13 at 19:02
-
Rather than having me try to explain and say something stupid, here's a brief explanation: http://math.berkeley.edu/~mjv/Lecture32.pdf – Random Variable Apr 23 '13 at 23:06
-
@RandomVariable: ah, that was not trivial to me. Not sure how it applies here though, although you might have seen the reference to "multiply connected domains," which is what we have here. – Ron Gordon Apr 23 '13 at 23:14
-
I don't think the theorem is useful in this particular case. But we basically have the same setup. So my contention is that the residue at infinity is the ILT and is equal to the integral around $C_{i}$. I don't know. – Random Variable Apr 24 '13 at 00:09
-
2It seems to me that the res at infty collapses all of the residue calculations to the pole at the origin when making the substitution $s=1/w$. Does this even make sense here? i don't know - and I am getting too tired to think about whether it does. – Ron Gordon Apr 24 '13 at 00:12
-
First thanks for your solution. May you explain me how did you get the integral over the line below the real axis? – Vahid May 07 '13 at 03:06
-
@vahidroomi: I think I made that clear in the above derivation. I substituted $s=e^{i \pi} x$ and the multivaluedness of the square root prevented cancellation with the integral above the real axis. – Ron Gordon May 07 '13 at 04:33
-
Thanks for your response. I have a question. When you get the functional form for the product of Bessels, I think the integral becomes $R[\int_0^\pi d \theta e^{\sqrt{p^2-q^2}\cos(\theta-i\beta)}]$ (I mean "-" instead of "+"). Because $\cos(i\beta)=\cosh(\beta)$ and $\sin(i\beta)=-\frac{1}{i}\sinh(\beta)$. Am I right? If yes, does this affect to the functional form? Thanks again (May I have your email address?) – Vahid May 08 '13 at 02:04
-
@vahidroomi: You may be right - even so, it does not affect the final result. I can set up a chat room if you prefer; that might be better. If not, my address is rlgordonma at gmail dot com. – Ron Gordon May 08 '13 at 02:14
-
Thanks again. I have an other question. When you get the functional form for the product of Bessels, May you explain me the statement "This integral is independent of β; to see this, differentiate with respect to β and note that we are taking the real part of the integral." please? – Vahid May 14 '13 at 04:48
-
1@vahidroomi: when you take the derivative with respect to $\beta$, you get the real part of $i$ times a real number, which is zero. – Ron Gordon May 14 '13 at 07:06
-
1@vahidroomi: please accept the solution if it has been useful to you. – Ron Gordon May 14 '13 at 07:07
-
Thank you so much Ron I truly appreciate your help. – Vahid May 15 '13 at 01:39