I see many people ask a lot of questions while they are pairing socks: Here, here, here, and here you can find some nice examples.
Some days ago I had a similar situation. I was pairing socks following the method "I take one random sock of the pile and I either put it in a row of distinct socks, or I pair it with an existing element of this row". Assuming I have $n$ distinct pairs of socks, I had the following situation: my first 7 random choices were all different. So, I had a line of 7 distinct socks before I could find a match. On the 8th choice, I found my first match. I thought that the probability to get this sequence had to be really small.
Some days later I was remembering that situation and I wondered how many socks I had. And I don't know it. Hence, I did some computations to figure it out, but they are not conclusive:
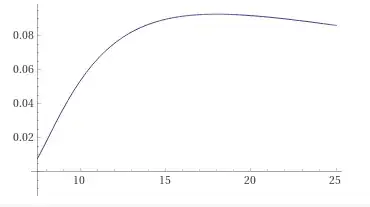
What is the probability that, given $n$ pairs of socks, you get 7 different in a row, and then one repeated? If I didn't make any mistake, this should be $ P(n) = \frac{56(n-5)(n-6)(n-7)}{(2n-1)(2n-3)(2n-5)(2n-7)} $
And the maximum is close to n=18. So, if I had to bet to a single number, I'd say I had 18 pairs of socks.
However...
This graph is clearly skewed to the right. If I had to bet to get "the best approximation", I'd compute the expected value. And here it comes my problem: which is the expected value of socks I have?
$ E(n) = \Sigma_{n\ge 8} n \frac{56(n-5)(n-6)(n-7)}{(2n-1)(2n-3)(2n-5)(2n-7)} = +\infty $
So, the expected value of pairs of socks I had is infinity, which clearly it is not, because I don't have enough space to store them.
Could you help me find how many socks do I have, please? Thank you! (please, don't tell me to go and count how many socks do I actually have in my house. Doing maths is by far much more fun :-) ).
P.S. How can it be nobody created the "socks" tag yet???