Is there a way to find the four tangents that two rotated ellipses share?
I believe that if two ellipses do not intersect and do not contain one another, they will have four tangents in common and I wish to find these tangents. I know how to complete the same process with circles and wish to do the same with ellipses.
Let us suppose that the ellipses are given by $f_1(x,y)=c_1$ and $f_2(x,y)=c2$. We seek points $(x_1,y_1)$ and $(x_2,y_2)$ such that the lines through those points are mutually tangent to the ellipsies. Clearly, $(x_1,y_1)$ must satisfy $f_1(x_1,y_2)=c_1$ and similiarly for the second point. Furthermore, the gradients of $f_1$ and $f_2$ must be parallel at their respective points. This yields $\nabla f_1(x_1,y_1) = \lambda \nabla f_2(x_2,y_2)$. Finally, we need the line through the points to perpendicular to the gradient vectors. This yields a total of five equations in the five unkowns $x_1$, $y_1$, $x_2$, $y_2$, and $\lambda$.
Let's apply this in the specific case $$x^2 - x*y+y^2 = 4$$ and $$2x^2+x*y+3y^2 = 1.$$
These ellipses do intersect, but I think that's no problem. The equations are sufficiently complicated that I think I'll do this with Mathematica.
f1[x_, y_] = x^2 - x*y + y^2;
f2[x_, y_] = 2 x^2 + x*y + 3 y^2;
grad1[x_, y_] = {D[f1[x, y], x], D[f1[x, y], y]};
grad2[x_, y_] = {D[f2[x, y], x], D[f2[x, y], y]};
eqs = Flatten[{
f1[x1, y1] == 1,
f2[x2, y2] == 4,
({x1, y1} - {x2, y2}).grad1[x1, y1] == 0,
Thread[grad1[x1, y1] == lambda*grad2[x2, y2]]
}];
pts = {{x1, y1}, {x2, y2}} /. NSolve[eqs, {x1, y1, x2, y2, lambda}]
(* Out: {
{{1.11372, 0.820906}, {1.37585, 0.122754}},
{{0.601823, 1.15435}, {-0.245408, 1.17882}},
{{-1.11372, -0.820906}, {-1.37585, -0.122754}},
{{-0.601823, -1.15435}, {0.245408, -1.17882}}} *)
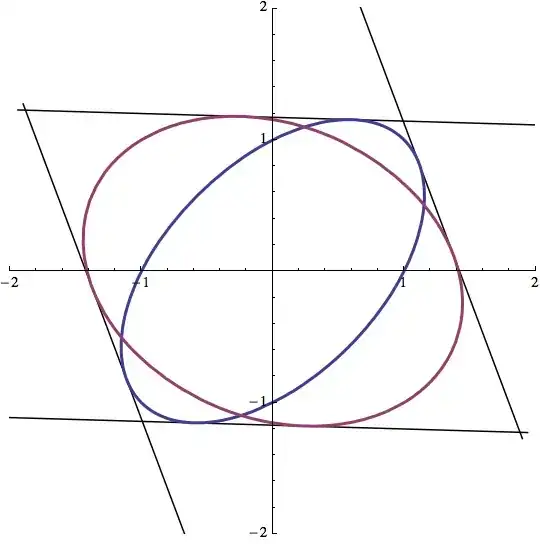
You can use Solve rather than NSolve but the resulting expressions are quite complicated. Let's visualize, as well.
line[{pt1_, pt2_}] := ParametricPlot[t*pt1 + (1 - t) pt2, {t, -2, 3},
PlotRange -> 2, PlotStyle -> Black];
lines = line /@ pts;
cp = ContourPlot[{
f1[x, y] == 1,
f2[x, y] == 4
}, {x, -3, 3}, {y, -3, 3},
ContourStyle -> {{Thick, ColorData[1, 1]}, {Thick,
ColorData[1, 2]}}];
Show[Flatten[{lines, cp}], PlotRange -> 2]
Expanding on WimC’s comment, this problem is dual to the problem of finding the intersection of a pair of conics. That is, if the two nondegenerate conics are represented by $3\times3$ homogeneous matrices $A$ and $B$, and lines are represented by homogeneous vectors $\mathbf l = [\lambda, \mu, \tau]^T$, so that the implicit equation of the line is $\mathbf l^T\mathbf x = 0$, the common tangents to the two conics are the solutions of the system $\mathbf l^TA^*\mathbf l = \mathbf l^TB^*\mathbf l = 0$. For nondegenerate conics, the dual conic matrix is any nonzero multiple of the inverse of the conic’s matrix (such as the adjugate). Of course, since any multiple of $\mathbf l$ represents the same line (these are homogeneous vectors, after all), if there are any solutions at all, then there will be an infinite number of them, so it’s helpful to add another simple constraint such as $\lambda+\mu+\tau = 1$. If you know that none of the tangents can pass through the origin, another simple way to constrain the solutions is to set $\tau=-1$.
Using the example from Mark McClure’s answer, we have $$A = \begin{bmatrix} 1 & -\frac12 & 0 \\ -\frac12 & 1 & 0 \\ 0&0&-1\end{bmatrix} \\ B = \begin{bmatrix} 2 & \frac12 & 0 \\ \frac12 & 3 & 0 \\ 0&0&-4 \end{bmatrix}.$$ (Note that I’m using the constant terms from the Mathematica code, which are swapped from those in the text of the answer.) Inverting these and multiplying by some arbitrary-looking scalars to make things look tidier, we get $$A^* = 3 A^{-1} = \begin{bmatrix} 4 & 2 & 0 \\ 2 & 4 & 0 \\ 0&0&-3 \end{bmatrix} \\ B^* = \frac{23}2 B^{-1} = \begin{bmatrix} 6&-1&0 \\ -1&4&0 \\ 0&0&-\frac{23}8 \end{bmatrix}.$$ The resulting system of equations is $$4 \lambda ^2+4 \lambda \mu +4 \mu ^2-3 \tau ^2 = 0 \\ 6 \lambda ^2-2 \lambda \mu +4 \mu ^2-\frac{23}8\tau ^2 = 0.$$ In this case both ellipses surround the origin, so we set $\tau = -1$ and solve. Turning to Mathematica, we obtain the solutions
{{lambda -> 0.0246484, mu -> 0.853438},
{lambda -> -0.0246484, mu -> -0.853438},
{lambda -> -0.703267, mu -> -0.264046},
{lambda -> 0.703267, mu -> 0.264046}}
which you can verify are the same lines as those computed in Mark McClure’s answer.
If you don’t have handy software for computing solutions to systems of second-degree equations, Jürgen Richter-Gebert presents an algorithm for finding the intersections of two conics in his Perspectives on Projective Geometry, which is outlined in this answer.
Assuming, for the sake of argument, the ellipse is centered and rotated about the origin (if it weren't, the same principle would apply, but the math would be more complex), the original, un-rotated ellipse can be modeled as a parametric equation:
$$x(t)=a\cos(t),y(t)=b\sin(t)\space 0\le t<2\pi$$
Now rotate it by multiplying it by the rotation matrix:
$$ \begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \\ \end{bmatrix}\begin{bmatrix} a\cos(t) \\ b\sin(t) \\ \end{bmatrix} $$
The resulting parametric equation for the rotated ellipse is
$$x(t)=a\cos(\theta)\cos(t)-b\sin(\theta)\sin(t)$$ $$y(t)=a\sin(\theta)\cos(t)+b\cos(\theta)\sin(t)$$
The tangent to any parametric curve is equal to $\frac{y'(t)}{x'(t)}$, so take the derivatives of each set of parametric equations, equate their ratios, and solve for t (remember that $\theta$ is a constant). That should give you the point where both their tangents are equal.
