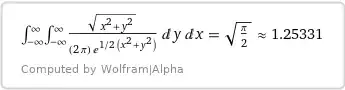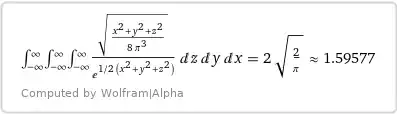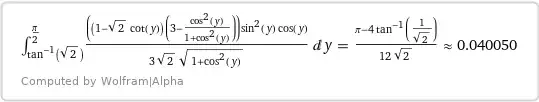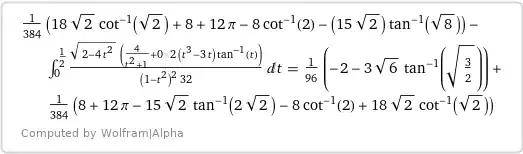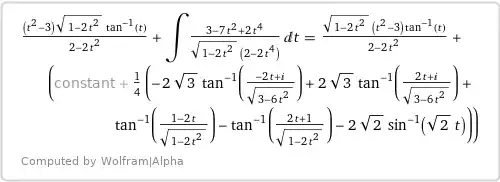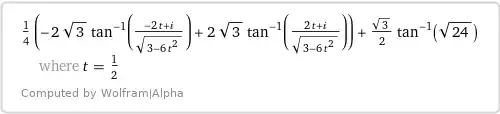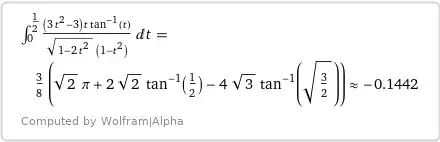Closed-form of $\mathbb E(\|G\|_\infty)$ where $G\sim\mathcal N(0,\mathbf{Id}_n)$.

Question

Let $I_n = \mathbb E(\|G\|_\infty)$, i.e. $$I_n = (2\pi)^{-\frac{n}{2}}\int_{x\in\mathbb R^n}\|x\|_\infty e^{-\frac{1}{2}\|x\|_2^2}\,dx.$$ I wonder if I can get its closed-form. By symmetry I got $$I_n = 2n\sqrt{\frac{2}{\pi}}\int_0^\infty xe^{-x^2}\operatorname{erf}(x)^{n-1}\,dx,$$ and then by integration by parts, for $n\ge2$, $$I_n = \frac{2\sqrt2}{\pi}n(n-1)\int_0^\infty e^{-2x^2}\operatorname{erf}(x)^{n-2}\,dx,$$ where $\operatorname{erf}$ is the error function.

These two formulas give me

$$I_1 = \sqrt{\frac{2}{\pi}},\quad I_2 = 2\sqrt{\frac{1}{\pi}},\quad I_3 = \frac{12}{\pi\sqrt\pi}\arctan\frac{\sqrt2}{2}.$$

In this step, I think a general closed-form is almost impossible, so I post here to see if anyone has a better approach (at least for $I_4$).

---

Update

Series expansion of $I_4$: $$I_4 = \frac{8\sqrt2}{\pi^2}\sum_{n=0}^{\infty}\left(\frac43\right)^n\frac{n!}{(2n+1)!}\,\Gamma(n+3/2)\,{}_2F_1(1/2,-n;3/2;1/4).$$

By the way $$I_n = \sqrt2n\int_0^1t^{n-1}\operatorname{erf}^{-1}(t)\,dt \,=\!\!\!?\; \sqrt2n\sum_{k=0}^\infty a_k \left(\frac{\sqrt\pi}{2}\right)^{2k+1}\frac1{2k+n+1},$$ where $a_k$ is the $k$-th coefficient of the Maclaurin series of $\operatorname{erf}^{-1}(2x/\sqrt\pi)$ (see InverseErf).

Well, I don't really know the behavior of $(a_k)$, but numerically the series does converge. I don't think this will lead to anything though.

---

Let me explain a little about this problem.

Imagine we have $n$ points to throw at 0 at the real axis, and the resulted position of one point is determined by $\mathcal N(0,1)$. We want to study the behavior of the farthest distance from 0.

This distance $D = \|G\|_\infty$ is determined by the density function defined below

$$f:x \mapsto n\sqrt{\frac2\pi}\,\exp\left(-\frac{x^2}2\right) \operatorname{erf}^{n-1}\frac{x}{\sqrt2} \mathbb1_{x\ge0}.$$

(For fun one can check that $\int_0^\infty f(x)\,dx=1$.)

And now, what we want to know is, how to calculate $\mathbb E(D)$ (at least when $n=4$)?

---

@YuriNegometyanov has given a formula for $\mathbb E(\|G\|_2)$. Even though it's not quite the topic, let's write it down as well:

$$\mathbb E(\|G\|_2) =\sqrt2\,\frac{\Gamma\left(\dfrac{n+1}2\right)}{\Gamma\left(\dfrac n2\right)}.$$

---

A jupyter notebook to calculate numerical results.

---

So from the series expansion of $I_4$ mentioned above (and tons of calculation), I got: $$I_4 = \frac{24}{\pi\sqrt\pi}\arctan\frac{1}{2\sqrt2}.$$ This is kind of interesting since the form is similar to $I_3$. Maybe a general closed-form is in fact possible?

Answer 1

$\color{brown}{\textbf{The task statement.}}$

By the symmetry, such integrals can be calculated via integrals over the hyper-octant, i.e. in the forms of $$M_n = E\big(\|G\|_2\big) = \left(\dfrac2\pi\right)^{\large\frac n2} \int\limits_0^\infty\int\limits_0^\infty\dots\int\limits_0^\infty\int\limits_0^\infty r\, e^{^{\large-\frac12r^2}}\,\text dx_1\,\text dx_2\dots\text dx_{n-1}\text dx_n,\tag1$$

$$I_n = E\big(\|G\|_\infty\big) = \left(\dfrac2\pi\right)^{\large\frac n2} \int\limits_0^\infty\int\limits_0^\infty\dots\int\limits_0^\infty\int\limits_0^\infty \max\limits_{j=1\dots n}\{x_j\}\, e^{^{\large-\frac12r^2}}\,\text dx_1\,\text dx_2\dots\text dx_{n-1}\text dx_n,$$

$$I_n = n!\left(\dfrac2\pi\right)^{\large\frac n2} \int\limits_0^\infty\int\limits_0^\infty\dots\int\limits_0^\infty\int\limits_0^\infty \prod\limits_{j=2\dots n}h(x_{j-1}-x_j) x_1\, e^{^{\large-\frac12r^2}}\,\text dx_1\,\text dx_2\dots\text dx_{n-1}\text dx_n,\tag{2}$$ where $\;h(t)\;$ is the Heaviside transition function.

$\color{brown}{\textbf{The hyperspherical coordinate system.}}$

In the hyperspherical coordinate system \begin{cases} x_n=r\cos\varphi_{n-1}\\ x_{n-1} = r\sin\varphi_{n-1}\cos\varphi_{n-2}\\ \dots\\ x_{2} = r\sin\varphi_{n-1}\dots\sin\varphi_{2}\cos\varphi_{1}\\ x_{1} = r\sin\varphi_{n-1}\dots\sin\varphi_{2}\sin\varphi_{1},\tag3 \end{cases} or \begin{cases} x_1=rp_1,\quad x_j=rc_{j-1}p_j,\quad x_n=rc_{n-1},\quad c_j =\cos\varphi_{j},\quad s_j=\sin\varphi_j,\\[4pt] p_j =\sin\varphi_j\sin\varphi_{j+1}\dots\sin\varphi_{n-1}=q_{j,n-1}, \quad j=1\dots n-1,\\[4pt] q^\,_{kl} =\sin\varphi_k\sin\varphi_{k+1}\dots\sin\varphi_l,\quad \\[4pt] p^\,_{jk}=(p_j)'_{\varphi_k}=q^\,_{j,k-1}\,c_kp^\,_{j+1},\quad k=j\dots n-1.\tag4 \end{cases}

The Jacobian equals to $$J=\begin{vmatrix} rp_{11} & rp_{12} & rp_{13} & rp_{14} & \dots & rp_{1,n-1} & p_1\\ -rp_{1} & rc_1p_{22} & rc_1p_{23} & rc_1p_{24} & \dots & rc_1p_{2,n-1} & c_1p_2\\ 0 & -rp_{2} & rc_2p_{33} & rc_2p_{34} & \dots & rc_2p_{3,n-1} & c_2p_3\\ 0 & 0 & -rp_{3} & rc_3p_{44} & \dots & rc_3p_{4,n-1} & c_3p_4\\ & \dots & & & \dots & & \dots\\ 0 & 0 & 0 & 0 & \dots & rc_{n-2}p_{n-1,n-1} & c_{n-2}p_{n-1}\\ 0 & 0 & 0 & 0 & \dots & -rp_{n-1} & c_{n-1}\tag5 \end{vmatrix},$$ then $$J= \dfrac{r^{n-1}}{c_1}\prod\limits_{j=1}^{n-2}p_{j+1} \begin{vmatrix} c_1 & s_1c_2& q_{12}c_3 & q_{13}c_4 & \dots & q_{1,n-2}c_{n-1} & p_1\\ -s_1c_1 & c^2_1c_2 & c^2_1s_2c_{3} & c^2_1q_{23}c_4 & \dots & c^2_1q_{2,n-2}c_{n-1} & c_1^2p_2\\ 0 & -s_2 & c_2c_3 & c_2s_3c_{4} & \dots & c_2q_{3,n-2}c_{n-1} & c_2p_3\\ 0 & 0 & -s_{3} & c_3c_{4} & \dots & c_3q_{4,n-2}c_{n-1} & c_3p_4\\ & \dots & & & \dots & & \dots\\ 0 & 0 & 0 & 0 & \dots & c_{n-2}c_{n-1} & c_{n-2}p_{n-1}\\ 0 & 0 & 0 & 0 & \dots & -s_{n-1} & c_{n-1}\\ \end{vmatrix}$$

$$= \dfrac{r^{n-1}}{c_1}\prod\limits_{j=1}^{n-2}p_{j+1} \begin{vmatrix} c_1 & s_1c_2& q_{12}c_3 & q_{13}c_4 & \dots & q_{1,n-2}c_{n-1} & p_1\\ 0 & c_2 & s_2c_{3} & q_{23}c_4 & \dots & q_{2,n-2}c_{n-1} & p_2\\ 0 & -s_2 & c_2c_3 & c_2s_3c_{4} & \dots & c_2q_{3,n-2}c_{n-1} & c_2p_3\\ 0 & 0 & -s_{3} & c_3c_{4} & \dots & c_3q_{4,n-2}c_{n-1} & c_3p_4\\ & \dots & & & \dots & & \dots\\ 0 & 0 & 0 & 0 & \dots & c_{n-2}c_{n-1} & c_{n-2}p_{n-1}\\ 0 & 0 & 0 & 0 & \dots & -s_{n-1} & c_{n-1}\\ \end{vmatrix}$$ $$= \dots = r^{n-1}\prod\limits_{j=1}^{n-2}p_{j+1},$$ $$J = r^{n-1}\prod\limits_{j=1}^{n-1}\sin\varphi_j^{j-1}.\tag6$$

$\color{brown}{\textbf{The first integral.}}$

Since $$A(n)=\int\limits_0^\infty r^n e^{-\frac12r^2}\text dr = 2^{^{\large\frac{n-1}2}}\Gamma\left(\dfrac{n+1}2\right),\tag7$$

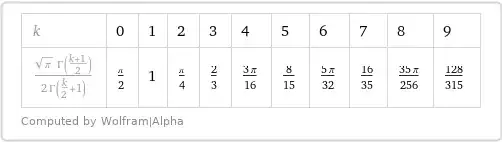
$$\Phi_2(k) = \int\limits_0^{^{\large \frac\pi2}}\,\sin^k\varphi\,\text d\varphi =\dfrac{\sqrt\pi\, \Gamma\left(\dfrac{k+1}2\right)}{2 \Gamma\left(\dfrac{k+2}2\right)},\tag8$$

then $$M_n = \left(\dfrac2\pi\right)^{^{\large\frac n2}}A(n)\prod\limits_{k=1}^{n-1}\Phi_2(k-1) = \sqrt2\,\dfrac{\Gamma\left(\dfrac{n+1}2\right)}{\Gamma\left(\dfrac n2\right)}.\tag9$$

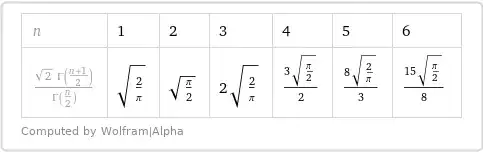
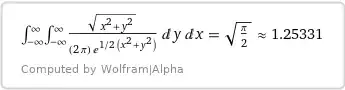
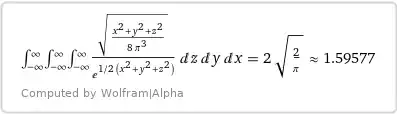
$\color{brown}{\mathbf{The\ second\ integral,\ n=1\dots 4.}}$

From $(2),(6)$ should $$I_1 = \sqrt{\frac2\pi}\,\int\limits_0^\infty xe^{-\frac12x^2}\,\text dx = \sqrt{\frac2\pi}\,.\tag{10a}$$ $$I_n = {n!}\left(\dfrac2\pi\right)^{^{\large\frac n2}} A(n)\Phi_\infty(n-1),\tag{11}$$ where $$\Phi_\infty(k) = \int\limits_{\large ^\pi/_4}^{\large^\pi/_2} \int\limits_{\text{ arccot }c_1}^{\large^\pi/_2}\;\dots \int\limits_{\text{ arccot }c_{k-1}}^{\large^\pi/_2} s_1s^2_2\dots s^k_k \,\text d\varphi_k\dots\,\text d\varphi_2\,\text d\varphi_1, \tag{12}$$ $$\text{ arccot }c_j = \arccos\dfrac{c_j}{\sqrt{1+c_j^2}} = \dfrac12 \arccos\dfrac{c_j^2-1}{c_j^2+1} = \dfrac12 \arcsin\dfrac{2c_j}{c_j^2+1},\tag{13a}$$ $$\text{ arccot }\dfrac1{\sqrt 2} = \arctan\sqrt 2 = \arccos\dfrac1{\sqrt3} = \dfrac12 \arccos\dfrac13 = \dfrac12 \arcsin\dfrac{2\sqrt2}3,\tag{13b}$$

$$\int \sin^k \varphi \,\text d\varphi = \begin{cases} \dfrac{2\varphi-\sin 2\varphi}4\,,\;k=2\\[4pt] \dfrac{\cos^3\varphi-3\cos\varphi}3\,,\;k=3\\[4pt] \dfrac{\sin 2\varphi \cos 2\varphi -4\sin 2\varphi+6\varphi}{16}\,,\;k=4.\tag{13c} \end{cases} $$

The angle limits should provide the integration over all non-increasing sequences $\;\{x_j\}.$

Then $$\Phi_\infty(2) = \int\limits_{\large^\pi/_4}^{\large^\pi/_2}\sin\varphi\,\text d\varphi = \dfrac1{\sqrt2},\tag{14b}$$ $$\Phi_\infty(3) = \int\limits_{\large^\pi/_4}^{\large^\pi/_2} \int\limits_{\text{arccot }c_1}^{\large^\pi/_2} \sin\varphi_1\sin^2\varphi_2\,\text d\varphi_2\,\text d\varphi_1 \\[4pt] = \int\limits_{\large^\pi/_4}^{\large^\pi/_2} \dfrac{2\varphi_2 -\sin 2\varphi_2}4 \bigg|_{\text{arccot }c_1}^{\large^\pi/_2} \sin\varphi_1\,\text d\varphi_1\\[4pt] = \dfrac12\int\limits_0^{\large^1/_{\sqrt2}}\left(\arctan c_1 + \dfrac {c_1}{1+c_1^2}\right)\,\text dc_1 = \dfrac12 c_1 \arctan c_1\bigg|_0^{\large ^1/{\sqrt2}},$$ $$\Phi_\infty(3)= \dfrac{\text{ arccot }\sqrt2}{2\sqrt2}\tag{14c}$$ (see also WA result),

$$\Phi_\infty(4) = \int\limits_{\large^\pi/_4}^{\large^\pi/_2} \int\limits_{\text{arccot }c_1}^{\large^\pi/_2}\; \int\limits_{\text{arccot }c_2}^{\large^\pi/_2} \sin\varphi_1\sin^2\varphi_2\sin^3\varphi_3 \,\text d\varphi_3\,\text d\varphi_2\,\text d\varphi_1 \\[4pt] = \int\limits_{\arctan\sqrt2}^{\large^\pi/_2} \int\limits_{\large^\pi/_4}^{\arccos\cot\varphi_2}\; \int\limits_{\text{arccot }c_2}^{\large^\pi/_2} \sin\varphi_1\sin^2\varphi_2\sin^3\varphi_3 \,\text d\varphi_3\,\text d\varphi_1\,\text d\varphi_2\\[4pt] = \int\limits_{\arctan\sqrt2}^{\large^\pi/_2} \left(\dfrac1{\sqrt2}-\cot\varphi_2\right) \dfrac13\left(\cos^3\varphi_3-3\cos\varphi_3\right)\bigg|_{\large \arccos\frac{\cos\varphi_2}{\sqrt{1+\cos^2\varphi_2}}}^{\large^\pi/_2} \sin^2\varphi_2 \,\text d\varphi_2\\[4pt] = \dfrac{\sqrt2}6 \left(\arctan\dfrac{\sin y}{\sqrt{2-\sin^2 y}} - \dfrac{\cos^2 y (\sin y - \sqrt2 \cos y)}{\sqrt{2-\sin^2 y}}\right) \bigg|_{\arctan\sqrt2}^{\large^\pi/_2},$$ $$\Phi_\infty(4)= \dfrac{\pi - 4\text{ arccot }\sqrt2}{12\sqrt2} = \dfrac{\text{arccot }(2\sqrt2)}{6\sqrt2}\tag{14d}$$ (see also WA result).

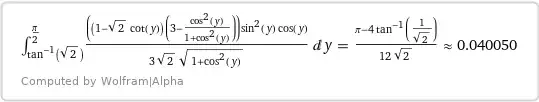
Therefore,

$$I_2 = 2!\cdot\frac2\pi\,A(2)\Phi_\infty(2) = \frac{4}\pi\cdot\sqrt{\frac\pi2}\,\frac1{\sqrt2} = \frac2{\sqrt\pi},\tag{10b}$$

$$I_3 = 3!\cdot\sqrt{\frac8{\pi^3}}\,A(3)\Phi_\infty(3) = 12\sqrt{\frac2{\pi^3}}\cdot2\,\dfrac{\text{ arccot }\sqrt2}{2\sqrt2} = \frac{12\text{ arccot }\sqrt2}{\pi\sqrt\pi},\tag{10c}$$

$$I_4 = 4!\cdot\frac4{\pi^2}\,A(4)\Phi_\infty(4) = \frac{96}{\pi^2}\cdot3\sqrt{\dfrac\pi2}\,\dfrac{\text{arccot }(2\sqrt2)}{6\sqrt2},$$ $$I_4 = \frac{24\text{ arccot }(2\sqrt2)}{\pi\sqrt\pi}.\tag{10d}$$

$\color{brown}{\mathbf{The\ second\ integral,\ n=5.}}$

Taking in account $(13a-c),$ one can get $$\Phi_\infty(5) = \int\limits_{\large^\pi/_4}^{\large^\pi/_2} \int\limits_{\text{arccot }c_1}^{\large^\pi/_2}\; \int\limits_{\text{arccot }c_2}^{\large^\pi/_2}\; \int\limits_{\text{arccot }c_3}^{\large^\pi/_2} \sin\varphi_1\sin^2\varphi_2\sin^3\varphi_3\sin^4\varphi_4 \,\text d\varphi_4\,\text d\varphi_3\,\text d\varphi_2\,\text d\varphi_1 \\[4pt] = \int\limits_{\arctan\sqrt2}^{\large^\pi/_2} \int\limits_{\large^\pi/_4}^{\arccos\cot\varphi_2} \int\limits_{\text{arccot }c_2}^{\large^\pi/_2}\quad \int\limits_{\text{arccot }c_3}^{\large^\pi/_2} \sin\varphi_1\sin^2\varphi_2\sin^3\varphi_3\sin^4\varphi_4 \,\text d\varphi_4\,\text d\varphi_3\,\text d\varphi_1\,\text d\varphi_2 \\[4pt] = \int\limits_{\arctan\sqrt2}^{\large^\pi/_2}\quad \int\limits_{\text{arccot }c_2}^{\large^\pi/_2}\; \left(\dfrac1{\sqrt2}-\cot\varphi_2\right) \dfrac1{16}\left(\sin2\varphi_4\cos2\varphi_4 - 4\sin2\varphi_4 + 6\varphi_4\right)\bigg|_{\text{arccot }c_3}^{\large^\pi/_2}\\ \times\sin^2\varphi_2\sin^3\varphi_3 \,\text d\varphi_3\,\text d\varphi_2\\[4pt] = \int\limits_{\arctan\sqrt2}^{\large^\pi/_2}\quad \int\limits_{\text{arccot }c_2}^{\large^\pi/_2}\; \dfrac{\sqrt2\,\sin^2\varphi_2-\sin2\varphi_2}{16}\\ \times\left(3\arctan\cos\varphi_3+\dfrac{4\cos\varphi_3}{1+\cos^2\varphi_3} +\dfrac{3\cos\varphi_3\sin^2\varphi_3}{(1+\cos^2\varphi_3)^2}\right) \sin^3\varphi_3\,\text d\varphi_3\,\text d\varphi_2\\[4pt] = \int\limits_{\large^\pi/_3}^{\large^\pi/_2}\quad \int\limits_{\arctan\sqrt2}^{\arccos\cot\varphi_3}\; \dfrac{\sqrt2\,\sin^2\varphi_2-\sin2\varphi_2}{16}\\ \times\left(3\arctan\cos\varphi_3+\dfrac{3\cos\varphi_3}{1+\cos^2\varphi_3} +\dfrac{2\cos\varphi_3}{(1+\cos^2\varphi_3)^2}\right) \sin^3\varphi_3\,\text d\varphi_2\,\text d\varphi_3\\[4pt] = \dfrac{\sqrt2}{64}\int\limits_{\large^\pi/_3}^{\large^\pi/_2}\quad \left(2\varphi_2 - \sin 2\varphi_2 + \sqrt2 \cos 2\varphi_2\right) \bigg|_{\arctan\sqrt2}^{\arccos\cot\varphi_3}\; \times\left(3\arctan\cos\varphi_3+\dfrac{3\cos\varphi_3}{1+\cos^2\varphi_3} +\dfrac{2\cos\varphi_3}{(1+\cos^2\varphi_3)^2}\right) \sin^3\varphi_3\,\text d\varphi_3\\[4pt] = \dfrac{\sqrt2}{32}\int\limits_{\large^\pi/_3}^{\large^\pi/_2}\quad \left(\sqrt2\cot^2\varphi_3 - \cot\varphi_3 \sqrt{1-\cot^2\varphi_3} + \arccos \cot\varphi_3 -\arctan\sqrt2\right) \times\left(3\arctan\cos\varphi_3+\dfrac{3\cos\varphi_3}{1+\cos^2\varphi_3} +\dfrac{2\cos\varphi_3}{(1+\cos^2\varphi_3)^2}\right) \sin^3\varphi_3\,\text d\varphi_3\\[4pt] = \dfrac{\sqrt2}{64}\int\limits_{\large^\pi/_3}^{\large^\pi/_2}\quad \left(\sqrt2\cot^2\varphi_3 - \cot\varphi_3 \sqrt{1-\cot^2\varphi_3} + \arccos \cot\varphi_3 -\arctan\sqrt2\right) \times\,\text d\left(\cos 2\varphi_3 + 2(\cos^3\varphi_3-3\cos\varphi_3)\arctan\cos\varphi_3+\dfrac{4}{1+\cos^2\varphi_3}\right)$$

(see also WA check),

$$\Phi_\infty(5) \;\overset{\text{IBP}}{=\!=} \; \dfrac{3\sqrt2 \text{ arccot}\sqrt2}{64} + \dfrac{\sqrt2}{32} \int\limits_{\large^\pi/_3}^{\large^\pi/_2}\quad \left(\sqrt2\cot\varphi_3 - \sqrt{1-\cot^2\varphi_3}\right) \times \left(2\cos^2\varphi_3 -1 + 2(\cos^3\varphi_3-3\cos\varphi_3) \arctan\cos\varphi_3+\dfrac{4}{1+\cos^2\varphi_3}\right)\dfrac{\text d\varphi_3}{\sin^2\varphi_3}\\[4pt] = \dfrac{3\sqrt2 \text{ arccot}\sqrt2}{64} + \dfrac{\sqrt2}{32} \int\limits_0^{\large^1/_2}\quad \left(\sqrt2c_3 - \sqrt{1-2c^2_3}\right)\\ \times \left(2c^2_3 -1 + 2(c^3_3-3c_3) \arctan c_3+\dfrac{4}{1+c^2_3}\right)\dfrac{\text dc_3}{(1-c^2_3)^2}\\[4pt] = \dfrac{12\pi + 18\sqrt2 \text{ arccot}\sqrt2 - 8\text{ arccot }2 - 15\sqrt2 \arctan(2\sqrt2) -12\sqrt6 \arctan\sqrt{^3/_2}}{384}\\ - \dfrac{\sqrt2}{16} \int\limits_0^{\large^1/_2}\quad \sqrt{1-2c^2_3}(c^3_3-3c_3) \arctan c_3 \dfrac{\text dc_3}{(1-c^2_3)^2}, $$

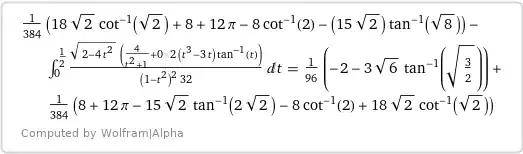
wherein $$\int\limits_0^{\large^1/_2}\quad \sqrt{1-2t^2}(t^3_3-3t) \arctan t \dfrac{\text dt}{(1-t^2)^2}\\[4pt] \;\overset{\text{IBP}}{=\!=} -\dfrac{11\sqrt2\text{ arccot }2}{12} + \dfrac18 ((4\sqrt3-\sqrt2)\pi - 2\arctan(2\sqrt2) - 4\sqrt3\arctan(2\sqrt6)) + \int\limits_0^{\large^1/_2} \dfrac{t(3 t^2-4)\arctan t}{\sqrt{1 - 2 t^2}(1-t^2)}\,\text dt =-\dfrac{11\sqrt2\text{ arccot }2}{12} + \dfrac14 ((2\sqrt3+\sqrt2)\pi - \arctan(2\sqrt2) - 2\sqrt3\arctan(2\sqrt6)) + \dfrac34 (\sqrt2 \text{ arccot }2 - 2\sqrt3 \arctan\sqrt{\dfrac32} - \int \limits_0^{\large^1/_2} \dfrac{t \arctan t}{\sqrt{1 - 2 t^2}(1-t^2)}\,\text dt ,$$

=

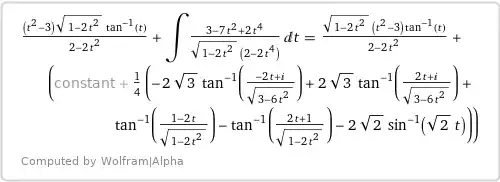
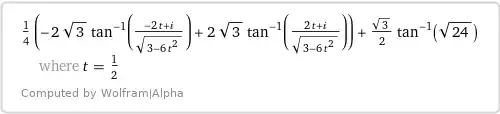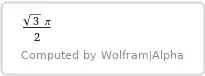
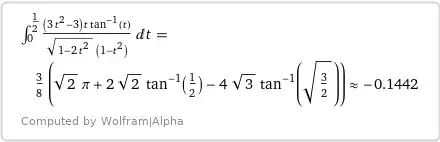
$$- \int\limits_0^{\large^1/_2} \dfrac{t \arctan t}{\sqrt{1 - 2 t^2}(1-t^2)}\,\text dt = \int\limits_{\large^1/_{\sqrt2}}^1 \dfrac{\arctan\sqrt{\dfrac{1-u^2}2}} {1+u^2}\,\text du = \int\limits_{\large^1/_{\sqrt2}}^1 \int\limits_{0}^{\large\sqrt{\frac{1-u^2}2}} \dfrac{\text dv\,\text du}{(1+v^2)(1+u^2)}\\[4pt] = \int\limits_0^{\text{arccot}\sqrt2} \int\limits_{{\large^1/_{\sqrt2}}\sec\psi}^{\large^1/_{\sqrt{\cos^2\psi + 2\sin^2\psi}}} \dfrac{\rho\,\text d\rho\,\text d\psi}{(1+\rho^2\cos^2\psi)(1+\rho^2\sin^2\psi)}\\[4pt] =\left|\genfrac{}{}{0}{}{s=\rho^{-2},}{w = 2\psi}\right| = \int\limits_0^{2\text{ arccot}\sqrt2} \int\limits_{\frac12(3-\cos w)}^{1+\cos w} \dfrac{\text ds\,\text dw}{(1+2s)^2-\cos^2w}\\[4pt] = \dfrac14\int\limits_0^{2\text{ arccot}\sqrt2} (\ln4 - \ln(4-2\cos w) + \ln(3+\cos w)-\ln(3+3\cos w)) \dfrac{\text dw}{\cos w}\\[4pt] = \dfrac14\int\limits_0^{2\text{ arccot}\sqrt2} (- \ln(1-\frac12\cos w) + \ln(1+\frac13\cos w)-\ln(1+\cos w)) \dfrac{\text dw}{\cos w}\\[4pt] =|w=2\arctan q| =\int\limits_0^{\large^1/_{\sqrt2}} (\ln(1+q^2)+\ln(2+q^2)+\ln 2-\ln(3+q^2)-\ln 3)\dfrac{dq}{2-2q^2}\\[4pt] =J\left(\dfrac1{\sqrt2}\right)- J(0)\approx 0.05721\,19956\,66783\,53930\,89922\,14090\,04283\,86906\,04 ,$$ wherein splitting both of the numerator and the denominator leads to the heavy closed form of the antiderivative $\;J(q),$

Therefore, $$\Phi_\infty(5)\approx 0.00505\,68737\,62649\,75165\,77798\,44133\,63992\,99350\,04542,\tag{14e}$$

$$I_5 = 5!\cdot\sqrt{\frac{32}{\pi^5}}\,A(5)\Phi_\infty(5) = 480\sqrt{\frac2{\pi^5}}\cdot8\,\Phi_\infty(5),$$ $$I_5\approx 1.56983\,37172\,15214\,46376\,24670\,41826\,20871\,99091.\tag{10e}$$

Answer 2

Let $J(a,n) = \int_0^\infty e^{-at}\operatorname{erf}^n\sqrt t\,dt$ for $a>0$.

Let $J_n=J(1,n)$, we have then $I_n = n\sqrt{\frac{2}{\pi}}J_{n-1}$.

By some equalities, we have the recurrence relation below:

$$J(a,0)=\frac1a,\quad J(a,1)=\frac1{a\sqrt{a+1}},$$ $$J(a,n)=J(a,n-2)-\frac{4}{\pi}\int_0^1\frac{1}{1+s^2}J\left(1+s^2+a,n-2\right)\,ds.$$

Then by some calculation, we have

$$J(a,2)=\frac{4}{\pi}\frac1{a\sqrt{a+1}}\arctan\frac1{\sqrt{a+1}},$$ and $$J(a,3)=\frac{4}{\pi}\frac1{a\sqrt{a+1}}\arctan\frac{1-b}{1+b},\text{ where }b=\frac{a}{a+4}\sqrt{\frac{a+3}{a+1}}.$$

(By the way, for fun one can prove that $$2\arctan\frac{5-\sqrt2}{5+\sqrt2}=3\arctan\frac{1}{2\sqrt2},$$ which shows up in $I_4$.)

We can also give an expression of $J_4$ (which gives $I_5$): \begin{align} J_4&=J_2-\frac{4}{\pi}\int_0^1\frac{1}{1+s^2}J\left(2+s^2,2\right)\,ds\\ &=J_2-\left(\frac{4}{\pi}\right)^2\int_0^1\frac{1}{1+s^2}\frac{1}{2+s^2}\frac{1}{\sqrt{3+s^2}}\arctan\frac{1}{\sqrt{3+s^2}}\,ds. \end{align}

As you can see, these become more and more complicated. I really don't think there's a closed-form for $I_n$ when $n\ge5$.

---

Alternatively, we also have $$J_n=\sum_{k=0}^n\left(-1\right)^k\binom{n}{k}C_k,$$ where $$C_k=\mathbb E\left[\phi(U)\right]=\pi^{-k}\int_{u\in\mathbb R^k}\phi(u)\prod_{i=1}^k\frac{1}{1+u_i^2}\,du,$$ $$\phi(u)=\frac{1}{1+\sum_{i=1}^k\left(1+u_i^2\right)},$$ and $U=(U_i)_{1\le i\le k}$ is a random vector of independent $\operatorname{Cauchy}(0,1)$ variables.

This might give us a global view of what happens in that recurrence relation (which I believe is unhelpful for a general closed-form).

(By the way, the formula of $\mathbb E(\|G\|_2)$ given by @YuriNegometyanov can be easily found using $\chi^2$-distribution.)

---

A little simplification (see here). $$J(a,3) = \frac{12}{\pi}\frac1{a\sqrt{a+1}}\left(\arctan\sqrt{\frac{a+3}{a+1}}-\frac\pi4\right).$$