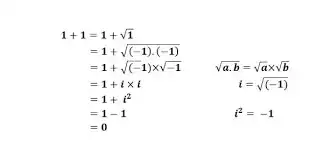The proof tacitly assumes that there is a function $sqrt:\mathbb{C}\rightarrow\mathbb{C}$ (which it calls "$\sqrt{\cdot}$") with the following two properties:
A: $sqrt$ gives square roots: for all $z$ we have $sqrt(z)^2=z$.
B: $sqrt$ distributes over multiplication: for all $z_0,z_1$ we have $sqrt(z_0)\cdot sqrt(z_1)=sqrt(z_0\cdot z_1)$.
I'll call such a function (if it exists) a good square rooter.
If there were such a function, then the proof would work - so in fact what's being shown is that no such function exists. This can be a stumbling point because of course over $\mathbb{R}_{\ge 0}$ there is such a function, namely the function sending $x$ to its unique nonnegative square root.
OK, so what is it about $\mathbb{C}$ as opposed to $\mathbb{R}_{\ge0}$ that makes the former have no good square rooter?
Well, it turns out that the issue is exactly that elements of $\mathbb{C}$ have multiple square roots in $\mathbb{C}$ in general, whereas each element of $\mathbb{R}_{\ge0}$ has exactly one square root in $\mathbb{R}_{\ge0}$. As soon as we're forced to "make a choice," we lose any hope of having a good square rooter.
To be precise:
Suppose $A$ is a commutative semiring in which every element has at least one square root. Then the following are equivalent:
- Every element in $A$ has exactly one square root.
- There is a good square rooter $sqrt_A:A\rightarrow A$.
Proof: The direction $2\rightarrow 1$ is basically just the argument in the OP! Suppose we have a good square rooter $sqrt_A$, and pick $a,b,c\in A$ with $a^2=b^2=c$. We have $$sqrt_A(c)=sqrt_A(a)\cdot sqrt_A(a)=sqrt_A(b)\cdot sqrt_A(b)$$ by condition B of good-square-rooter-ness, but we also have $$sqrt_A(a)\cdot sqrt_A(a)=a\mbox{ and }sqrt_A(b)\cdot sqrt_A(b)=b$$ by condition A. Put together we get $a=b$ as desired.
In the other direction, suppose $(1)$ holds. Then we can define a function $s: A\rightarrow A$ by $s(a)=$ the unique $b$ with $b^2=a$. This trivially satisfies condition A of good-square-rooter-ness, so we just have to show that $$s(a)\cdot s(b)=s(a\cdot b)$$ for every $a,b\in A$.
And this is nice and easy! By definition of $s$, we have $$[s(a)s(b)]^2=[s(a)^2][s(b)^2]ab=[s(ab)]^2.$$ So $s(a)s(b)$ and $s(ab)$ are elements of $A$ which square to the same thing (namely $ab$), which means .... that they're equal by our assumption that we're in case $(1)$.
"But wait!", you might reasonably say, "what about $\mathbb{R}_{\ge0}$? Positive real numbers do have multiple square roots even though we have a good square rooter in $\mathbb{R}_{\ge0}$. What gives?"
The point is that we get extra square roots for positive reals only when we step outside of $\mathbb{R}_{\ge 0}$. Within $\mathbb{R}_{\ge0}$ itself, every element has exactly one square root. The proposition is very carefully phrased to be about what's going on inside the commutative semiring $X$, not about how $X$ sits inside some yet larger commutative semiring.
So we always have to pay attention to where the solutions to various equations exist!