3

While studying some physics problems, I stumbled upon this experimental equality:

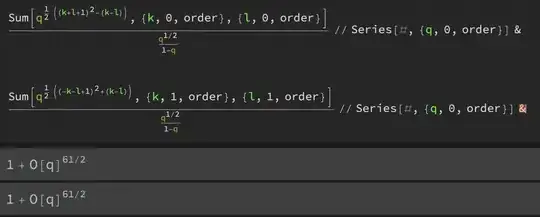
$$ \sum_{k, \ell = 0}^{+\infty} q^{\frac{ 1 }{ 2 }[( k + \ell + 1)^2 - (k- \ell)]} = \frac{ \sqrt{q} }{ 1-q } \ . $$

I have checked this equality with Mathematica to a very high order:

enter image description here

However, I wonder how to prove it? Is it (or its generalization) discussed somewhere? (the sum smells like some $\Theta$-function, but I don't know where to look).

Update:

It turns out that the series above equals the false theta function $g_{1,1,1}(-1, -q, q)$ discussed in this paper https://www.sciencedirect.com/science/article/pii/S0022314X18300611 . It remains to educate myself about these special function

Lelouch
  • 637

1 Answers1

3

Rewrite $$ \sum_{k, \ell = 0}^{+\infty} q^{\frac{ 1 }{ 2 }[( k + \ell + 1)^2 - (k- \ell)]} = \frac{ \sqrt{q} }{ 1-q } $$ as $$ \sum_{k, \ell = 0}^{+\infty} x^{( k + \ell + 1)^2 - (k- \ell)} = \frac{x }{ 1-x^2 } $$ RHS is the sum of the series $$\sum _{n=1}^{\infty } x^{2 n-1}=\frac{x }{ 1-x^2 };\;0\le x<1 $$ I say that the sequence $$\{( k + \ell + 1)^2 - (k- \ell)\};\; k,\ell\in\mathbb{N}$$ is exactly the sequence of the odd positive integers.

Expand the expression to get

$$k^2+2 k \ell+k+\ell^2+3 \ell+1$$

We want to prove that, subtracting $1$ and dividing by $2$, the expression $$f(k,\ell)=\frac{1}{2}\left(k^2+2 k \ell+k+\ell^2+3 \ell\right)$$ gives, for $k=0,1,2,\ldots;\;\ell=0,1,2,3,\ldots$ all the natural numbers only once.

That is, the function $f:\mathbb{N}^2\to\mathbb{N}$ is a bijection.

The proof is here. And a more detailed reference is here.

Raffaele
  • 26,371