2

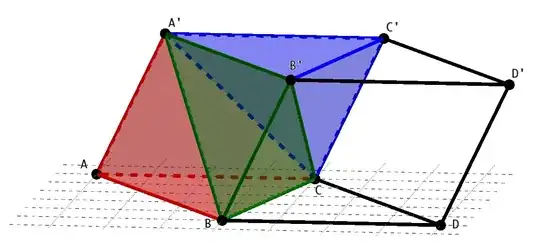
Now some of the readers in a rush might think that this a duplicate of Tetrahedron volume relation to parallelepiped and pyramid

But it is not. In the froe-mentioned question it has been asked to derive a mathematical relation between the 2, which I already have derived(using the scalar triple product). But, I couldn't visually wrap my mind around the fact that you can fit 6 tetrahedrons in a parallelepiped ? Am I interpreting the result right ? that you can fit 6 tetrahedrons whose volume are equal into a parallelepiped whose volume is the sum of all of those tetrahedrons ? I have looked all over the internet, but couldn't find a figure that would help me understand this visually, and develop a visual intuition for it. A figure would be much appreciated.

Koustubh Jain
  • 207
  • You have used the word $\mathbf{fit}$ twice in your problem statement. Do you mean $\mathbf{pack}$, when you mention $\mathbf{fit}$? – YNK Oct 03 '20 at 15:55

1 Answers1

9

You can see below how three equal-volume tetrahedra can be combined to form a prism with triangular base $ABCA'B'C'$. If you want a prism with a parallelogram as base, just add points $D$ and $D'$ and repeat the same scheme: you'll end with six tetrahedra packed into the prism.

enter image description here

Intelligenti pauca
  • 50,470
  • 4
  • 42
  • 77