Definition of a Factorial

Question

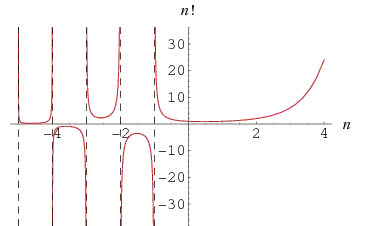
Now I have always been rather intrigued with factorial, at first, in high school, teachers told me that factorials are only defined for whole numbers. As I studied, I found factorials for positive reals and negative fractions. But the integral with which we define factorial falls flat on the negative integers.

why is that we can find the factorial of (-1/2) and root(3) but not for -1 or -2? Does this go against the definition of a factorial? If yes, what IS the definition of a factorial because children are never taught it and it clouds their reasoning and perception of the topic.

Welcome to Mathematics Stack Exchange. Cf. gamma function, which is defined for all complex numbers except non-positive integers. For positive integers $n$, $\Gamma(n)=(n-1)!$ — J. W. Tanner, Sep 10 '20 at 10:40
but gamma function isn't equivalent to factorial function, its just something that is loosely correlated — Louis Jones, Sep 10 '20 at 10:41
Well, the usual Gamma function is the factorial function when defined as that improper integral and continued analitically to the negative non-integer numbers (I'm referring here just to the real part of the function), so it is not only loosely correlated indeed. — DonAntonio, Sep 10 '20 at 10:48
Possible duplicate of: Why is Euler's Gamma function the “best” extension of the factorial function to the reals? — Vepir, Sep 10 '20 at 10:54

score 1 · Answer 1 · 2020-09-10T11:49:10.920

Children are only taught the factorial of naturals because the definition is elementary (though $0!=1$ deserves special comments).

When you want to extend it to reals, a natural way is with the integral

$$I_n=\int_0^\infty x^ne^{-x}dx$$ as it verifies the recurrence

$$I_n=\int_0^\infty x^ne^{-x}dx=-\left. x^ne^{-x}\right|_0^\infty+n\int_0^\infty x^{n-1}e^{-x}dx=nI_{n-1}$$ and $I_n=n!$.

As the integral keeps a meaning with $n$ positive real, this is taken for the extension.

Now for the negatives, it makes sense to retain the recurrence

$$(n-1)!=\frac{n!}n,$$ resulting in infinite values for the negative integers.

score 0 · Answer 2 · answered Sep 10 '20 at 11:32

The recursive definition of the factorial $(n+1)! = n! \cdot (n+1)$ can be rearranged to deduce $$n! = \dfrac{(n+1)!}{n+1}$$

This is one way to work out that $0!=1$, taking $n=0$ in the above. However, if we try and do this for $(-1)!$, we get a problem: $$(-1)! = \dfrac{(-1+1)!}{-1+1} = \dfrac{0!}{0} = \dfrac{1}{0}$$

But we can't divide by $0$, so we can't define $(-1)!$.

As noted in the comments, the gamma function $\Gamma$ is the "right" way to extend the factorial to non-integers. $\Gamma$ diverges at the negative integers, since it is required to satisfy $\Gamma(n+1) = \Gamma(n) \cdot (n+1)$, so the same argument as above applies.

Definition of a Factorial

2 Answers2