Here is a solution based on the computation of pairs of (common) tangents. This is done by using a powerful formula (ill) known as $(SS_1-T^2)=0$. Knowing this very general formula can be useful for treating potentially more complicated issues of a similar type, even if in this case it could be considered as "overkill". A drawback of this formula (but is it really one ?) is that it necessitates the use of a CAS (Computer Algebra System).
Let us first recall that the tangent in $(x_0,y_0)$ to a conic curve with equation
$$S(X):=ax^2+by^2+2cxy+2dx+2ey+f=0 \ \text{where} \ X=(x,y)\tag{1}$$
is
$$T(X,X_0):=axx_0+byy_0+c(xy_0+x_0y)+d(x+x_0)+e(y+y_0)+f=0\tag{2}$$
Now, the main formula, currently taught in the early 20th century, but largely unknown in 2020:
Theorem (formula $SS_1-T^2=0$): the cone issued from $(x_1,y_1)$ and tangent to a conic curve with equation (1) is given by formula:
$$S(X)S(X_1)-T(X,X_1)^2=0\tag{3}$$
Of course, in 2D, replace "cone" by "pair of tangent line equations". But it is important to know that this formula is generalizable to 3D and even nD.
A 3D example can be found here.
In our case, we are going to do the inverse path: we will be looking for points $X_0=(x_0,y_0)$ such that equation (3) is fullfilled for our 2 circles with equations, $S_1=0$ and $S_2=0$.
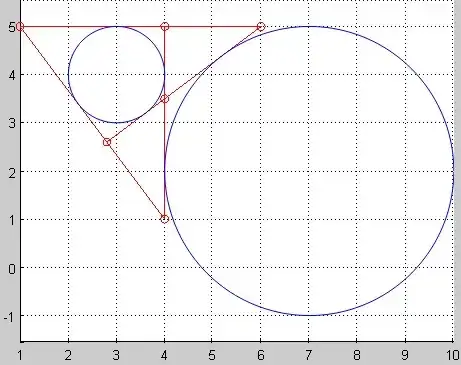
As we have $4$ common tangents, we must await $6=\binom{4}{2}$ pairs of tangents and in particular $6$ intersection points of these pairs of tangents that are depicted (red dots) in the figure, among which we will find the two dilation centers, the positive one and the negative one
$$(1,5) \ \text{and} \ (4,7/2)$$
More precisely, but without entering into the details, it suffices to compare the coefficients of $x^2$, $xy$ and $y^2$ in the expansions of $$S_1(X)S_1(X_0)-T_1(X,X_0)^2=0 \ \text{and} \ S_2(X)S_2(X_0)-T_2(X,X_0)^2=0$$ to get the following system :
$$\begin{cases}(y_0^2 - 8y_0 + 15)&=&a(y_0^2 - 4y_0 - 5)\\
(8x_0 + 6y_0 - 2x_0y_0 - 24)&=&a(4x_0 + 14y_0 - 2x_0y_0 - 28)\\
(x_0^2 - 6x_0 + 8)&=&a(x_0^2 - 14x_0 + 40)\end{cases}\tag{4}$$
($a$ being a proportionnality coefficient ; all this is to be done of course by a CAS).
(4) is a system of 3 equations with three unknowns. Its solutions are the 6 points:
$$(x_0,y_0)=(6,5),(4,1),(1,5),(4,5),(4,7/2), (14/5,13/5)$$
that we can see on the figure.
For a proof of the formula, see #278 (page 251) and #289 of the book by Loney
https://archive.org/details/elementsofcoordi00loneuoft
(not a recent one, I admit)
Connected: https://math.stackexchange.com/q/3764389