5

After trying to get my head around this for an embarrassingly long time, I think I need some help... We defined local (lyapunov) stability and asymptotic stability the following way:

An equilibrium $y^*$ of $\dot{y} = f(y)$ is called

  1. stable, if for each $\varepsilon$-neighbourhood $B_\varepsilon (y^*)$ there exists a $\delta$-neighbourhood $B_\delta(y^*)$ such that $$y_0 \in B_\delta(y^*) \implies y(t) \in B_\varepsilon (y^*) \forall t\geq t_0$$

  2. asymptotically stable, if $y^*$ is stable and there exist a $\mu$-neighbourhood $B_{\mu} (y^*)$ such that $$y_0 \in B_{\mu} (y^*) \implies \lim_{t \to \infty} y(t, y_0) = y^*$$

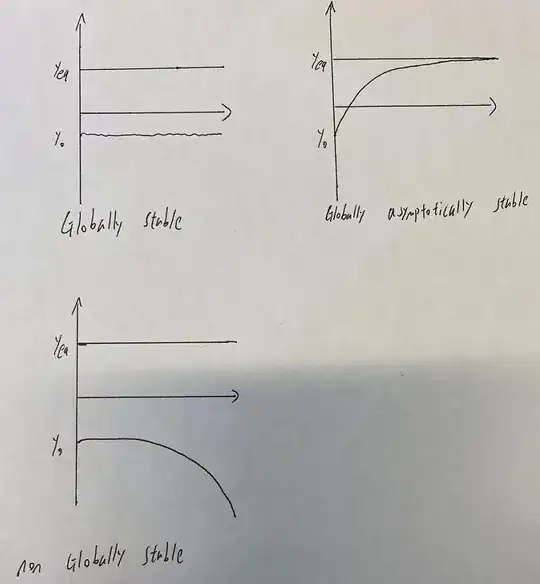
Ok so up to here both defintions make total sense to me. Now here comes my trouble: Later in the lecture we define "global stability" just with the following sentence:

"An equilibrium is called globally stable, if it is stable for (almost) all initial conditions, not just some which are close to the equilibrium $y^*$."

We don't introduce global asymptotic stability at all. But doesn't this definition of global stability imply $\lim_{t\to\infty} y(t, y_0) = y^* $ for all $y_0$? We also use this to prove global stability once. But wouldn't this be the definition of global asymptotic stability? What is the difference between the two? We go on to Lyapunov functions and mention there that under certain conditions you get global stability while if additionally $\dot V =0$ you get global asymptotic stability.

This course isn't really about stability analysis so we didn't go into depth at all, or provided any proofs but I would really like to understand the difference between global stability and global asymptotic stability. I've read everything on google and found nothing, so I probably don't see something extremely trivial. Any help is appreciated!

Mark Kamsma
  • 12,935
spindrift
  • 53

2 Answers2

3

"Global" and "asymptotical" are different attributes. Note that a stable equilibrium may not be an attractor. For instance, the solutions of: $$ x'=-y \\ y'=x $$ are the circles $x^2+y^2=r_0^2$ so the origin is stable because trajectories remain inside a bounded neighbourhood as small as desired (depending on the initial $r_0$), but they do not tend to the origin.

Since this system is linear, the stability is global, meaning there are no unbounded trajectories even if we start far from the origin. In contrast, for the one-dimensional system: $$ y'=y(1-y) $$ linearization shows that the equilibrium $y^*=1$ is stable and, in fact, asymptotically stable. However, this property is not global, e.g. the solution with initial condition $y_0=0$ is the constant trajectory $y(t)\equiv 0$ so $y(t)\notin B_{\frac{1}{2}}(1)$.

Miguel
  • 3,265
0

I have the same confusion about Globally stable and Globally asymptotically stable. I think this is because Globally stable does not have a clearly strictly mathematical definition, while Global asymptotic stability does have. (I search through the whole internet and cannot find the exact definition of Global stability. I will be very grateful if someone can provide it)

I am going to give my understanding of Globally stable and Globally asymptotically stable.

  1. Globally stable: A trajectory with an arbitrary initial point in the domain will remain a fixed distance from the equilibrium point. Formally, $y_{eq}$ is global stability if for any trajectory $y(t)$ with an initial point $y_0$, there always exists an $\epsilon >0$, such that $$y(t) \in B_\epsilon(y_{eq}) \quad \forall t\geq0$$
  2. Globally asymptotically stable: A trajectory with an arbitrary initial point in the domain will be additionally going toward the equilibrium point. Formally, $y_{eq}$ is globally stably if for any trajectory $y(t)$ with an initial point $y_0$, it satisfies $$\lim_{t \to \infty} y(t) = y_{eq}$$

There is a picture I drew to help illustrate the difference between non Globally stable, Globally stable, and Globally asymptotically stable.non Globally stable, Globally stable, and Globally asymptotically stable

Again, This is just my understanding, and I can't guarantee it is 100% correct, but it looks perfect to me for all my cases. Any comment or suggestion considering this post is welcome.

Reference:

  1. Chapter 3 Stability and Performance from a course note at Caltech
  2. Lyapunov method to prove stabbility
dawen
  • 395