Contour Integration: $\int_0^\infty\frac{1}{x^a(1-x)}\,dx$ for $0

Question

I've been trying to calculate $$\int_0^\infty\frac{1}{x^a(1-x)}\,dx\quad\text{with }0<a<1.$$I haven't had much luck. I tried taking the branch cut with of the positive reals and estimating that way, but I wasn't sure how to handle the poles at $z=0$ and $z=1$ when dealing with branch cuts. I also looked at the Wikipedia page to try to get some insight, but I didn't see any similar examples with the contour closing in on poles that are on a branch cut.

Answer 1

You use an almost-keyhole contour, except that you indent both paths above and below the real axis with a small semicircle to avoid the pole at $z=1$:

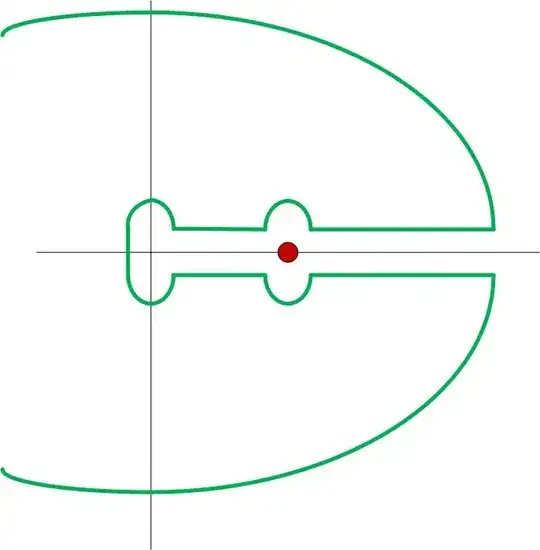
In doing this, you end up with not $4$, but $8$ contour segments. I will avoid writing them all out by noting that the integrals over the outer circular arc and inner circular arc at the origin vanish in the limits of their radii going to $\infty$ and $0$, respectively. We are left with

$$\oint_C dz \frac{z^{-a}}{1-z} = \int_{\epsilon}^{1-\epsilon} dx \frac{x^{-a}}{1-x} + i \epsilon \int_{\pi}^0 d\phi\, e^{i \phi} \frac{(1+\epsilon e^{i \phi})^{-a}}{-\epsilon e^{i \phi}} + \int_{1+\epsilon}^{\infty} dx \frac{x^{-a}}{1-x} \\+e^{-i 2 \pi a} \int_{\infty}^{1+\epsilon} dx \frac{x^{-a}}{1-x} +e^{-i 2 \pi a} i \epsilon \int_{2 \pi}^{\pi} d\phi\, e^{i \phi} \frac{(1+\epsilon e^{i \phi})^{-a}}{-\epsilon e^{i \phi}} +e^{-i 2 \pi a} \int_{1-\epsilon}^{\epsilon} dx \frac{x^{-a}}{1-x} $$

Combining like terms, we get

$$\oint_C dz \frac{z^{-a}}{1-z} = \left ( 1-e^{-i 2 \pi a}\right ) PV\int_{0}^{\infty} dx \frac{x^{-a}}{1-x} + \left ( 1+e^{-i 2 \pi a}\right ) i \pi = 0$$

because of Cauchy's Theorem. $PV$ denotes the Cauchy principal value. After a little algebra, the result is

$$PV\int_{0}^{\infty} dx \frac{x^{-a}}{1-x} = -i \pi \frac{1+e^{-i 2 \pi a}}{1-e^{-i 2 \pi a}}=-\pi \cot{\pi a}$$

EXAMPLE

Let's check the result for $a=1/2$. This would imply that

$$PV \int _{0}^{\infty} dx \frac{1}{\sqrt{x} (1-x)} = 0$$

Consider

$$\begin{align}\underbrace{\int_0^{1-\epsilon} dx \frac{1}{\sqrt{x} (1-x)}}_{x=1/u} &= \int_{1/(1-\epsilon)}^{\infty} \frac{du}{u^2} \frac{\sqrt{u}}{1-(1/u)} \\ &= -\int_{1+\epsilon}^{\infty} du \frac{1}{\sqrt{u} (1-u)}\end{align}$$

Thus

$$\int_0^{1-\epsilon} dx \frac{1}{\sqrt{x} (1-x)} + \int_{1+\epsilon}^{\infty} du \frac{1}{\sqrt{u} (1-u)} = 0$$

or

$$PV \int _{0}^{\infty} dx \frac{1}{\sqrt{x} (1-x)} = 0$$

as was to be demonstrated.

Answer 2

$\newcommand{\bbx}[1]{\,\bbox[15px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\on}[1]{\operatorname{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ $\ds{\bbox[5px,#ffd]{\large An\ Alternative:}}$ \begin{align} &\bbox[5px,#ffd]{% \left.{\rm P.V.}\int_{0}^{\infty}{\dd x \over x^{a}\pars{1 - x}} \,\right\vert_{\,a\ \in\ \pars{0,1}}} = -\,\Re\int_{0}^{\infty}{x^{-a} \over x - 1 + \ic 0^{+}}\,\dd x \\[5mm] = &\ \Re\int_{\infty}^{0}{\ic^{-a}\,\,y^{-a} \over \ic y - 1} \,\ic\,\dd y = -\,\Im\bracks{\ic^{-a}\int_{0}^{\infty} {\,y^{\pars{\color{red}{1 - a}} - 1} \over 1 - \ic y}\,\dd y} \end{align} I'll evaluate the last integral with the Ramanujan's Master Theorem. Note that $\ds{{1 \over 1 - \ic y} = \sum_{k = 0}^{\infty}\pars{\ic y}^{k} = \sum_{k = 0}^{\infty}\color{red}{\Gamma\pars{1 + k}\expo{-k\pi\ic/2}}\,\,{\pars{-y}^{k} \over k!}}$.

Then, \begin{align} &\bbox[5px,#ffd]{% \left.{\rm P.V.}\int_{0}^{\infty}{\dd x \over x^{a}\pars{1 - x}} \,\right\vert_{\,a\ \in\ \pars{0,1}}} \\[5mm] = &\ -\,\Im\pars{\ic^{-a}\,\,\Gamma\pars{1 - a}\braces{\Gamma\pars{1 -\bracks{1 - a}}\expo{\pars{1 - a}\pi\ic/2}\,}} \\[5mm] = &\ -\,\Re\bracks{\expo{-\pi a\ic}\,\, \Gamma\pars{1 - a}\Gamma\pars{a}} = -\cos\pars{\pi a}\,{\pi \over \sin\pars{\pi a}} \\[5mm] = &\ \bbx{-\pi\cot\pars{\pi a}} \\ & \end{align}