Based on this answer to the question "How to evaluate $ \int_0^\infty \frac{\log x}{(x^2+a^2)^2} dx $" and on this answer to the question "Evaluate $\int_0^\infty \frac {(\log x)^4dx}{(1+x)(1+x^2)}$". Instead of a function with $\log z$ on the numerator, we consider a function with $\log^2 z$. This is the very same method as that pointed to in the comments.
For $a,b>0$, this method gives the closed formula
$$
\int_{0}^{\infty }\frac{\log x}{\left( x+a\right) ^{2}+b^{2}}\,dx=\frac{1}{2b
}\arctan \left( \frac{b}{a}\right) \log \left( a^{2}+b^{2}\right) ,\qquad
a,b>0\tag{$\ast$}.
$$
We chose the multiple-valued function $f(z)$ with branch cut $\arg z=0$
defined as
$$
\begin{align*}
f(z) &=\frac{\log ^{2}z}{\left( z+a\right) ^{2}+b^{2}},\quad \text{with }
0<\arg z<2\pi ,\quad z=re^{i\theta } \\
&=\frac{\log ^{2}z}{\left( z-z_{1}\right) \left( z-z_{2}\right) }\qquad
z_{1}=-a+ib,\quad z_{2}=-a-ib,
\end{align*}
$$
and integrate it counterclockwise around the closed contour $\Gamma $
shown in the figure. This contour is indented around the branch point $O$
and consists of the circles $\gamma _{R}$ ($\left\vert z\right\vert =R$) and
$\gamma _{\varepsilon }$ ($\left\vert z\right\vert =\varepsilon $), $
0<\varepsilon <1<R$, and the segment $\left[ \varepsilon ,R\right] $
described in the positive sense above the $x$-axis and in the negative sense
below the $x$-axis.
$\qquad\qquad$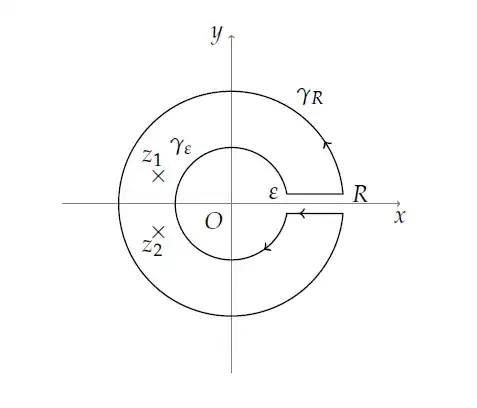
$$\text{Closed contour } \Gamma $$
On the upper edge, $\theta =0$ ($r\in \left[ \varepsilon ,R\right] $) and
$$
f(z)=\frac{\left( \log r\right) ^{2}}{\left( r+a\right) ^{2}+b^{2}}.
$$
On the lower edge, $\theta =2\pi $ ($r\in \left[ \varepsilon ,R\right] $) and
$$
f(z)=\frac{\left( \log \left( re^{i2\pi }\right) \right) ^{2}}{\left(
r+a\right) ^{2}+b^{2}}=\frac{\left( \log r+i2\pi \right) ^{2}}{\left(
r+a\right) ^{2}+b^{2}}.
$$
As such,
$$
\begin{align*}
I &=\lim_{\varepsilon \rightarrow 0,R\rightarrow \infty }\oint_{\Gamma}
\frac{\left( \log z\right) ^{2}}{\left( z+a\right) ^{2}+b^{2}}\,dz, \\
&=\int_{0}^{\infty }\frac{\left( \log r\right) ^{2}}{\left( r+a\right)
^{2}+b^{2}}\,dr-\int_{0}^{\infty }\frac{\left( \log \left( re^{i2\pi
}\right) \right) ^{2}}{\left( re^{i2\pi }+a\right) ^{2}+b^{2}}\,dr \\
&\quad+\lim_{R\rightarrow \infty }\int_{\gamma _{R}}\frac{\left( \log z\right)
^{2}}{\left( z+a\right) ^{2}+b^{2}}\,dz-\lim_{\varepsilon \rightarrow
0}\int_{\gamma _{\varepsilon }}\frac{\left( \log z\right) ^{2}}{\left(
z+a\right) ^{2}+b^{2}}\,dz \\
&=\int_{0}^{\infty }\frac{\left( \log r\right) ^{2}-\left( \log r+i2\pi
\right) ^{2}}{\left( r+a\right) ^{2}+b^{2}}\,dx \\
&=4\pi ^{2}\int_{0}^{\infty }\frac{1}{\left( r+a\right) ^{2}+b^{2}}
\,dr-i4\pi \int_{0}^{\infty }\frac{\log r}{\left( r+a\right) ^{2}+b^{2}}\,dr
\end{align*}
$$
provided that
$$
\lim_{R\rightarrow \infty }\int_{\gamma _{R}}\frac{\left( \log z\right) ^{2}
}{\left( z+a\right) ^{2}+b^{2}}\,dz=\lim_{\varepsilon \rightarrow
0}\int_{\gamma _{\varepsilon }}\frac{\left( \log z\right) ^{2}}{\left(
z+a\right) ^{2}+b^{2}}\,dz=0,\quad \text{(see below).}
$$
By the residue theorem,
$$
\begin{align*}
I &=2\pi i\left( \operatorname{Res}_{z=z_{1}}f(z)+
\operatorname{Res}_{z=z_{2}}f(z)\right) \\
&=2\pi i\left[ \operatorname{Res}_{z=z_{1}}\frac{
\left( \log z\right) ^{2}}{\left( z-z_{1}\right) \left( z-z_{2}\right) }+
\operatorname{Res}_{z=z_{2}}\frac{\left( \log z\right)
^{2}}{\left( z-z_{1}\right) \left( z-z_{2}\right) }\right] \\
&=2\pi i\left[ \frac{\left( \log z_{1}\right) ^{2}}{z_{1}-z_{2}}+\frac{
\left( \log z_{2}\right) ^{2}}{z_{2}-z_{1}}\right] \\
&=2\pi i\left[ \frac{\left( \log \left( -a+ib\right) \right) ^{2}}{i2b}-
\frac{\left( \log \left( -a-ib\right) \right) ^{2}}{i2b}\right] \\
&=\frac{\pi }{b}\left[ \log \left( -a+ib\right) \right] ^{2}-\frac{\pi }{b}
\left[ \log \left( -a-ib\right) \right] ^{2}
\end{align*}
$$
We now assume that $a,b>0$. Then
$$
\begin{align*}
I &=\frac{\pi }{b}\left[ \log \left( \left\vert -a+ib\right\vert \right)
+i\left( \pi -\arctan \left( \frac{b}{a}\right) \right) \right] ^{2} \\
&\quad-\frac{\pi }{b}\left[ \log \left( \left\vert -a-ib\right\vert \right)
+i\left( \pi +\arctan \left( \frac{b}{a}\right) \right) \right] ^{2} \\
&=\frac{\pi }{b}\left[ \frac{1}{2}\log \left( a^{2}+b^{2}\right) +i\left(
\pi -\arctan \left( \frac{b}{a}\right) \right) \right] ^{2} \\
&\quad-\frac{\pi }{b}\left[ \frac{1}{2}\log \left( a^{2}+b^{2}\right) +i\left(
\pi +\arctan \left( \frac{b}{a}\right) \right) \right] ^{2} \\
&=\frac{4\pi ^{2}}{b}\arctan \left( \frac{b}{a}\right) -i\frac{2\pi }{b}
\arctan \left( \frac{b}{a}\right) \log \left( a^{2}+b^{2}\right)
\end{align*}
$$
because
$$
\log \left( \left\vert -a+ib\right\vert \right) =\log \left( \left\vert
-a-ib\right\vert \right) =\frac{1}{2}\log \left( a^{2}+b^{2}\right) .
$$
Taking the imaginary part of $I$ we obtain $(\ast)$ in the form
$$
\text{Im }( I )=-4\pi \int_{0}^{\infty }\frac{\log r}{\left( r+a\right) ^{2}+b^{2}
}\,dr=-\frac{2\pi }{b}\arctan \left( \frac{b}{a}\right) \log \left(
a^{2}+b^{2}\right)
$$
Proof that $\int_{\gamma _{R}}f,\int_{\gamma _{\varepsilon }}f\rightarrow 0$. If $z$ is any point on $\gamma _{R}$,
$$
\begin{align*}
\left\vert f(z)\right\vert &=\frac{\left\vert \log z\right\vert ^{2}}{
\left\vert \left( z+a\right) ^{2}+b^{2}\right\vert },\qquad z=R\,e^{i\theta
},R>1,0<\theta <2\pi \\
&\leq \frac{\left( \log R+2\pi \right) ^{2}}{\left\vert z+\left(
-z_{1}\right) \right\vert \left\vert z+\left( -z_{2}\right) \right\vert }, \\
&\leq \frac{\left( \log R+2\pi \right) ^{2}}{\left\vert R-\sqrt{a^{2}+b^{2}}
\right\vert ^{2}}\leq M_{R}
\end{align*}
$$
where
$$
M_{R}=\frac{4\pi \log R+4\pi
^{2}+\log ^{2}R}{R^{2}+\left( a^{2}+b^{2}\right) -2R\sqrt{a^{2}+b^{2}}}
$$
because
$$
\left\vert z+\left( -z_{1}\right) \right\vert \geq \left\vert R-\left\vert
z_{1}\right\vert \right\vert ,\left\vert z+\left( -z_{2}\right) \right\vert
\geq \left\vert R-\left\vert z_{2}\right\vert \right\vert ,\left\vert
z_{1}\right\vert =\left\vert z_{2}\right\vert =\sqrt{a^{2}+b^{2}}.
$$
This means that
$$
\begin{align*}
\left\vert \int_{\gamma _{R}}f(z)\,dz\right\vert &\leq M_{R}\times \,2\pi R
\\
&=\frac{4\pi \log R+4\pi ^{2}+\log ^{2}R}{R^{2}+\left( a^{2}+b^{2}\right)
-2R\sqrt{a^{2}+b^{2}}}\times \,2\pi R\longrightarrow 0\qquad \left(
R\rightarrow \infty \right) .
\end{align*}
$$
Similarly, if $z$ is any point on $\gamma _{\varepsilon }$
$$
\begin{align*}
\left\vert f(z)\right\vert &=\frac{\left\vert \log z\right\vert ^{2}}{
\left\vert \left( z+a\right) ^{2}+b^{2}\right\vert },\qquad z=\varepsilon
\,e^{i\theta },0<\varepsilon <1,0<\theta <2\pi \\
&\leq \frac{\left( \log \varepsilon +2\pi \right) ^{2}}{\left\vert z+\left(
-z_{1}\right) \right\vert \left\vert z+\left( -z_{2}\right) \right\vert } \\
&\leq \frac{\left( \log \varepsilon +2\pi \right) ^{2}}{\left\vert
\varepsilon -\sqrt{a^{2}+b^{2}}\right\vert ^{2}}\leq M_{\varepsilon },
\end{align*}
$$
where
$$
M_{\varepsilon }=\frac{4\pi \log \varepsilon +4\pi ^{2}+\log
^{2}\varepsilon }{\varepsilon ^{2}+\left( a^{2}+b^{2}\right) -2\varepsilon
\sqrt{a^{2}+b^{2}}}
$$
and
$$
\begin{align*}
\left\vert \int_{\gamma _{\varepsilon }}f(z)\,dz\right\vert &\leq
M_{\varepsilon }\times \,2\pi \varepsilon \qquad z=\rho \,e^{i\theta },\rho
<1 \\
&\leq \frac{4\pi \log \varepsilon +4\pi ^{2}+\log ^{2}\varepsilon }{
\varepsilon ^{2}+\left( a^{2}+b^{2}\right) -2\varepsilon \sqrt{a^{2}+b^{2}}}
\times \,2\pi \varepsilon \longrightarrow 0\qquad \left( \varepsilon
\rightarrow 0\right) .
\end{align*}
$$
