A very interesting question: intersection point of $x^y=y^x$

Question

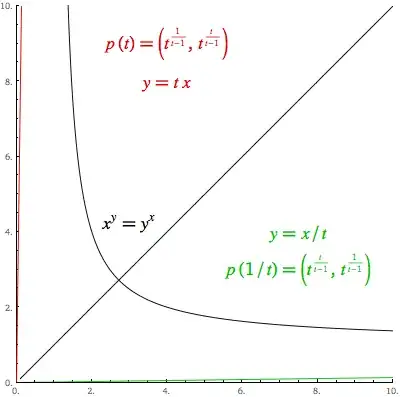
I've been investigating the Cartesian graph of $x^y=y^x$. Obviously, part of the graph is comprised of the line $y=x$ but there is also a curve that is symmetrical about the line $y=x$. (We can prove this symmetry by noting that the function $x^y=y^x$ is self-inverse; all self-inverse functions are symmetrical about the line $y=x$.)

An image of the graph is shown below:

I decided to find the intersection point and arrived at an intriguing result: the intersection point between the two curves is at $(e,e)$.

The following is my method: If the gradient of the line $y=x$ is $1$, the gradient of the curve at the intersection point must be $-1$ as it's a normal to the line (as it's symmetrical about the line). This means that at that point $\frac{dy}{dx}=-1$. Now to find $\frac{dy}{dx}$.

We have $x^y=y^x$. I then used a very powerful tehnique for differentiating these sorts of functions. We know that eg $$x^y=e^{\ln{x^y}}=e^{y\ln{x}}$$ and $$\frac{d}{dx}e^{f(x)}=f'(x)e^{f(x)}$$ Applying it to our function $x^y=y^x$ and using implicit differentiation and the product rule gives us: $$(\frac{dy}{dx}\times \ln x +\frac{y}{x})x^y=(\ln y +\frac{dy}{dx}\times \frac{x}{y})y^x$$ So $$\frac{dy}{dx}x^y\ln x +yx^{y-1}=\frac{dy}{dx}xy^{x-1}+y^x \ln y$$ Extensively rearranging gives: $$\frac{dy}{dx}=\frac{y^x \ln y -yx^{y-1}}{x^y \ln x -xy^{x-1}}$$ Let $\frac{dy}{dx}=-1$: $$y^x \ln y -yx^{y-1}=xy^{x-1}-x^y\ln x$$ But we know $x=y$ since we are at the intersection point with the line $y=x$: $$x^x \ln x -x^x=x^x-x^x\ln x$$ So $2x^x \ln x -2x^x=0$ $$2x^x(\ln x -1)=0$$ This means either $2x^x=0$ or $\ln x -1=0$ but we know $x^x$ is always greater than $0$ so $\ln x =1$, leaving us with: $$x=y=e$$ So I have my answer, but is there any other method of getting it? I have heard there is. Any help will be very welcome.

Thanks in advance

Answer 1

A Simple Approach

The simplest approach that I have found is to look at the intersections of $$ y=tx\qquad\text{and}\qquad x^y=y^x\tag1 $$ That is, $$ \begin{align} x^{tx}&=(tx)^x\tag{2a}\\[3pt] x^t&=tx\tag{2b}\\[3pt] x^{t-1}&=t\tag{2c}\\ x&=t^{\frac1{t-1}}\tag{2d}\\ y&=t^{\frac t{t-1}}\tag{2e} \end{align} $$ Explanation:
$\text{(2a)}$: $x^y=y^x$
$\text{(2b)}$: raise to the $\frac1x$ power
$\text{(2c)}$: divide by $x$
$\text{(2d)}$: raise to the $\frac1{t-1}$ power
$\text{(2e)}$: $y=tx$

Now, if we wish to find where $x=y$, let $t\to1$. That is, $$ \begin{align} x &=\lim_{t\to1}t^{\frac1{t-1}}\tag{3a}\\ &=\lim_{n\to\infty}\left(1+\frac1n\right)^n\tag{3b}\\[6pt] &=e\tag{3c} \end{align} $$ Explanation:
$\text{(3a)}$: $x=y$ when $t=1$
$\text{(3b)}$: $t=1+\frac1n$
$\text{(3c)}$: evaluate the limit

---

Further Musings

We can also compute $$ \begin{align} y &=\lim_{t\to1}t^{\frac t{t-1}}\tag{4a}\\ &=\lim_{n\to\infty}\left(1+\frac1n\right)^{n+1}\tag{4b}\\[6pt] &=e\tag{4c} \end{align} $$ Explanation:
$\text{(4a)}$: $x=y$ when $t=1$
$\text{(4b)}$: $t=1+\frac1n$
$\text{(4c)}$: evaluate the limit

Using the results from this answer, we see that $\left(1+\frac1n\right)^n$ is increasing and $\left(1+\frac1n\right)^{n+1}$ is decreasing, which means that $\left(1+\frac1n\right)^n\le e\le\left(1+\frac1n\right)^{n+1}$.

Thus, as $t\to1^+$, $(4)$ and $(5)$ show that $x\to e^-$ and $y\to e^+$.

Furthermore, if we substitute $t\mapsto1/t$, we get $$ \begin{align} t^{\frac1{t-1}} &\mapsto(1/t)^{\frac1{1/t-1}}\tag{5a}\\ &=t^{\frac t{t-1}}\tag{5b} \end{align} $$ and $$ \begin{align} t^{\frac t{t-1}} &\mapsto(1/t)^{\frac{1/t}{1/t-1}}\tag{6a}\\ &=t^{\frac1{t-1}}\tag{6b} \end{align} $$ That is, substituting $t\mapsto1/t$ swaps $x$ and $y$.

This means that, as $t\to1^-$, $x\to e^+$ and $y\to e^-$.

---

Relation to the Graph

Here is where these points sit on the graph as $t\to1^+$:

Answer 2

Not sure to understand well the question but if it provides any help, I think there is something missing in your analysis.

Your equation can be seen as $g(x,y) = x^{y} = y^{x} = f(x,y)$. You are looking for intersecting points or surfaces (x,y) in $\mathbb{R}^{3}$, since both $f(\cdot,\cdot)$ and $g(\cdot,\cdot)$ are 2D scalar fields. Otherwise, if you are thinking the expression $x^{y} = y^{x}$ as the equation of a curve in $\mathbb{R}$ (somehow you figure out to express $y = f(x)$ or $x = f(x)$, it doesn't make sense to talk about an intercept (or interception set) since you must provide another curve or surface.

The same applies with the fields $g$ and $f$. You must provide another equation since you have two unknowns.

The answer you got $(x,y) = (e,e)$ is the trivial answer, and works for any real $k \in \mathbb{R}$: $(x,y) = (k,k)$.

Answer 3

I don't know if this is what you are looking for, but I would go like this.

First rewrite the equation : $$x^y=y^x\Leftrightarrow y\ln(x)=x\ln(y)\Leftrightarrow \frac{\ln(x)}{x}=\frac{\ln(y)}{y}$$ Now consider the function $f(x)=\frac{\ln(x)}{x}$ defined on $(0,+\infty)$ and whose derivative is $f'(x)=\frac{1-\ln(x)}{x^2}$. This shows that $f$ induces two bijections $f_1:(0,e]\to (-\infty,\frac{1}{e}]$ and $f_2:[e,+\infty)\to[\frac{1}{e},0)$.

Now the locus $f(x)=f(y)$ can be divided in two curves, namely $y=f_1^{-1}(f(x))$ and $y=f_2^{-1}(f(x))$. (Note however that these two curves are not the obvious ones). And we are looking their intersection. Since the ranges of $f_1^{-1}$ and $f_2^{-1}$ are respectively $(0,e]$ and $[e,+\infty)$, the only possible value of $y$ for the intersection is $y=e$ which happen when $x=e$.

Answer 4

This is not exactly an answer, but part of your reasoning was a bit hand-wavy and I want to make it fully rigorous.

Your reasoning about the slopes of the two parts of the plot is intuitively correct, but needs proof. So it is clear that the slope of the first part of the plot is $1$ since this encompasses the solutions $x^x=x^x$, i.e, the identity map which has slope $1$ by definition. However, showing that the other branch of the plot has slope $-1$ is a bit more difficult. We need to show that

1: The relation $y^x-x^y=0$ is its own inverse

2: If a relation is its own inverse, its slope at a point $(x,y)$ is $-1$ if $x=y$, with the exception of the identity map.

The first point is rather easy and I'll leave it for you to do yourself. The second part, however, requires a bit of care. Any two variable relation can be summarized by the general equation $$f(x,y)=0$$ Well, not quite any, but I hope you get the idea. For example, the equation of a circle: $$x^2+y^2-r^2=0$$ We want to use information about $f$ to deduce $\frac{\mathrm{d}y}{\mathrm{d}x}$. Using a bit of knowledge from multivariable calculus, we know that the total derivative of a two-variable function $f$ in terms of an arbitrary variable $u$ is $$\frac{\mathrm{d} f}{\mathrm{d} u}=\frac{\partial f}{\partial x}\frac{\mathrm{d}x}{\mathrm{d}u}+\frac{\partial f}{\partial y}\frac{\mathrm{d}y}{\mathrm{d}u}$$ In the special case that $u=x$, $$\frac{\mathrm{d} f}{\mathrm{d} x}=\frac{\partial f}{\partial x}+\frac{\partial f}{\partial y}\frac{\mathrm{d}y}{\mathrm{d}x}$$ And similarly $$\frac{\mathrm{d} f}{\mathrm{d} y}=\frac{\partial f}{\partial x}\frac{\mathrm{d}x}{\mathrm{d}y}+\frac{\partial f}{\partial y}$$ If the relation is its own inverse, then $$f(x,y)=f(y,x)=0$$ Thus $$\frac{\mathrm{d} f}{\mathrm{d} x}=\frac{\partial f}{\partial x}+\frac{\partial f}{\partial y}\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d} f}{\mathrm{d} y}=\frac{\partial f}{\partial x}\frac{\mathrm{d}x}{\mathrm{d}y}+\frac{\partial f}{\partial y}$$ So $$\frac{\partial f}{\partial x}\left(1-\frac{\mathrm{d}x}{\mathrm{d}y}\right)=\frac{\partial f}{\partial y}\left(1-\frac{\mathrm{d}y}{\mathrm{d}x}\right)$$ But again, since $f(x,y)=f(y,x)=0$, $\frac{\partial f}{\partial x}=\frac{\partial f}{\partial y}$ if $x=y$, thus $$1-\frac{\mathrm{d}x}{\mathrm{d}y}=1-\frac{\mathrm{d}y}{\mathrm{d}x}$$ $$\frac{1}{\frac{\mathrm{d}y}{\mathrm{d}x}}=\frac{\mathrm{d}y}{\mathrm{d}x}$$ Therefore $\frac{\mathrm{d}y}{\mathrm{d}x}=\pm 1$. Excluding the only self-inverse relation with slope $1$, the identity map, we conclude $$\frac{\mathrm{d}y}{\mathrm{d}x}\big|_{(x,x)}=-1.$$

Following this, the rest of your reasoning is correct. Others have stated that this problem can be tackled using the product log, so I can't really think of another way of going about this problem. Good question though!

Answer 5

We are looking for solutions to $$ \exp(y\log x) = \exp(x\log y) \, . $$ Taking logs of both sides and rearranging, this equation becomes $$ \frac{x}{\log x}=\frac{y}{\log y} \, . $$ Consider the graph of $f(z)=z/\log z$:

Its unusual shape can be explained by a few observations:

• For $0<z<1$, $\log z$ is negative, so $f(z)$ is negative.
• As $z\to1$, $\log z \to 0$, and so the graph has an asymptote at $z=1$.
• For $z>1$, $\log z$ is positive, so $f(z)$ is positive.
• $f(z)$ is large when $\log z$ is small, or when $z$ is very large.

It is the final observation that gives us a hint as to why $f(z)$ has a local minimum. We can study the behaviour of $f(z)$ more closely by considering $$ f'(z) = \frac{\log z - 1}{\log^2z} \, . $$ For $1<z<e$, $f'(z)$ is negative; at $z=e$, $f'(z)$ is zero; and for $z>e$, $f'(z)$ is positive.

Now that we have proven that $f(z)$ has a local minimum at $(e,e)$, we can begin to examine your question more closely. Let $(x,\log x)$ and $(y,\log y)$ be arbitrary points that lies on the graph.

• Suppose $0<x<1$. Then, because $f(z)$ is one-to-one on the interval $(0,1)$, the only time when $f(x)=f(y)$ is when $x=y$.
• If $x>1$, then things are more complicated. Clearly, if $x=y$, then we still have $f(x)=f(y)$. However, if $1<x<e$, then there is a unique number $y\in(e,\infty)$ such that $f(x)=f(y)$. This is obviously still the case if the roles of $x$ and $y$ are interchanged.
• If $x$ is slightly smaller than $e$, then $y$ is either equal to $x$, or is only slightly larger than $e$. This means that the two sections of the graph get very close to each other as $x$ tends to $e$.
• In the limit, when $x=e$, the two parts of the graph coincide.

Answer 6

The equation is equivalent to

$$\frac{\log x}x=\frac{\log y}y.$$

The function

$$\frac{\log x}x$$

has a maximum at $x=e$ and for $x>0$

$$\frac{\log x}x=\frac{\log y}y$$ has two solutions in $x$.

Using Lambert's function,

$$-\frac1x\log\frac1x=\frac{\log y}y$$ and

$$e^{\log\frac1x}\log\frac1x=-\frac{\log y}y$$

and

$$\log\frac1x=W\left(-\frac{\log y}y\right).$$