Derivation of bounds of convergence of infinite tower

Question

If you want to solve for $$\large{x^{x^{.^{.^{.^.}}}}=2}$$ With an infinite tower of $x$
You say that there is a copy on top and say $x^2$=2 and then solve to get $x$=${\pm}{\sqrt{2}}$ .
but if you solve for : (using same technique )$$\large{x^{x^{.^{.^{.^.}}}}=4}$$
you again get $x$=${\pm}{\sqrt{2}}$ ( this can of course can not be true )

And so there is a theorem that states
If :$$\large{e^{-e} {\le}x{\le}} e^{1/e}$$ and $$\large{{1/e}{\le}y{\le} e}$$ for $x$ being the value that is infinitely exponentiated and y being a value that it converges to.
then
the infinite tower will converge to y

Since for the four case y>e it does not converge to 4 .And since the two case satisfies the inequalities it converges to 2

Q: I want to know how to rigorously derive these bounds

Answer 1

The OP says: this of course can not be true.
But that's only for the power tower as such. What seems to have been considered instead, however, is the inverse function of the tower: $$ y = x^{x^{.^{.^{.^.}}}} = x^y \quad \Longrightarrow \quad x = y^{1/y} $$ Scaling in $y$-direction is three times scaling in $x$-direction in the picture below, for good reasons.

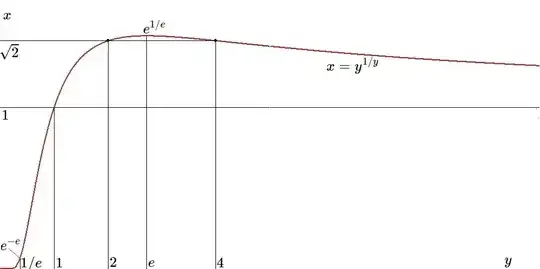
While the power tower itself is not defined outside the interval $e^{-e} \le x \le e^{1/e}$, the inverse function, when considered apart from the former, is defined, not only for $\,1/e \le y \le e\,$ but for a much larger domain, namely $\,0 \le y \lt \infty\,$. Details of function behaviour are described a great deal in the following MSE posting and its references:

• Why does ${x}^{x^{x^{x^{\,.^{\,.^{\,.}}}}}}$ bifurcate below $\sim0.065$?

It's easy to prove that $\,\lim_{y\to\infty} y^{1/y} = 1\,$. This means that $\,x = y^{1/y}\,$ has twofold solutions $\,y_{1,2}\,$ for $\,1 \lt x \lt e^{1/e}\,$, one $\,1 \lt y_1 \lt e\,$ and the other $\,e \lt y_2\,$, wich is anyway clear from the picture. Indeed the OP's solutions are among these: $\,1 \lt 2\lt e \lt 4\,$.

---

Numerically. Solutions of $\,y^{1/y}=x\,$ have been calculated by the (Delphi Pascal) program below. Values of $\,x\,$ are taken from a sample array, giving accompanying $\,y_{1,2}\,$ values with Newton's method. Initial $\,y_{1,2}\,$ are taken from previous steps, starting with the two known values from the question.

program edit;

function Newton(y12,x : double) : double;
const
  eps : double = 1.e-9;
var
  y : double;
begin
  y := y12;
  while abs(exp(ln(y)/y)-x) > eps do
    y := y - (exp(ln(y)/y)-x) * sqr(y)/(exp(ln(y)/y)*(1-ln(y)));
  Newton := y;
end;

procedure test;
const
  x : array[0..8] of double =
 (1.4, 1.3, 1.2, 1.1, 1.05, 1.02, 1.01, 1.001, 1.0001);
var
  y1,y2 : double;
  k : integer; 
begin
  y1 := 2; y2 := 4;
  for k := 0 to 8 do
  begin
    y1 := Newton(y1,x[k]);
    y2 := Newton(y2,x[k]);
    Writeln(x[k],' ==> (',y1,',',y2,')');
  end;
end;

begin
  test;
end.

Output:

 1.40000000000000E+0000 ==> ( 1.88666330624630E+0000, 4.41029279309327E+0000)
 1.30000000000000E+0000 ==> ( 1.47098895928257E+0000, 7.85706535100170E+0000)
 1.20000000000000E+0000 ==> ( 1.25773454121357E+0000, 1.47674583809828E+0001)
 1.10000000000000E+0000 ==> ( 1.11178201104165E+0000, 3.82287327653121E+0001)
 1.05000000000000E+0000 ==> ( 1.05270345488064E+0000, 9.28715283791938E+0001)
 1.02000000000000E+0000 ==> ( 1.02041238660200E+0000, 2.85536314597273E+0002)
 1.01000000000000E+0000 ==> ( 1.01010152374054E+0000, 6.51100334614211E+0002)
 1.00100000000000E+0000 ==> ( 1.00100100150234E+0000, 9.12312634995737E+0003)
 1.00010000000000E+0000 ==> ( 1.00010001000084E+0000, 1.16676997475209E+0005)

It is seen that the $\,y_1\,$ values near $\,y=1\,$ are close to $\,x\,$. Which should not be surprising, because $1^{1/1}=1$ and $\,\left. dx/dy\right|_{y=1}=1\,$. But I have no decent estimate for the "far away" solutions $\,y_2\,$.