4

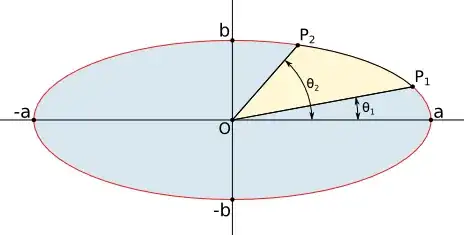
I'm attempting to draw a pie-chart programmatically, using an ellipse instead of a circle, but I'm having trouble calculating the correct angles for the slices. If it were a circle, I could use the percentage that the slice represents multiplied by $360$ degrees to obtain the accurate angles created by the slices.

Assume the following is known about an ellipse centered at the origin with a slice $s$:

  1. radii $a$ and $b$
  2. the percentage of the area that slice $s$ represents
  3. angle $\theta_1$, which is the angle from $0$ degrees to the beginning of the first edge of the slice (moving counter-clockwise).

How do you calculate the angle that slice $s$ creates from the center of the ellipse?

Note: Essentially, I would need to find either $\theta_2$ or the angle of the yellow-shaded slice depicted in this question:

enter image description here

Community
  • 1
mliberatore
  • 143
  • 2
    As a matter of programming, you might consider just computing the corresponding parts of a circular pie chart and then scale them down in the y direction. That doesn't answer your question though (but it should give you a hint). – Josephine Moeller Apr 24 '13 at 20:09

1 Answers1

4

The process given by Rahul Narain in the question you link to gives just what you want when inverted. Let $\theta_1$ and $\theta_2$ be as shown. He suggests scaling the ellipse vertically by a factor $\frac ab$ to make it a circle. If $p_1$ has coordinates $(p_{1x},p_{1y})$, its image $r_1$ will have coordinates $(p_{1x},\frac abp_{1y})$. Similarly, the image of $p_2$ will have coordinates $(p_{2x},\frac abp_{2y})$. The image of $\theta_1$ is then $\phi_1=\arctan \frac {ap_{1y}}{bp_{1x}}=\arctan [\frac ab \tan \theta_1$] and the image of $\theta_2$ is then $\phi_2=\arctan \frac {ap_{2y}}{bp_{2x}}=\arctan [\frac ab \tan \theta_2]$. You are asking that $\frac {\phi_2-\phi_1}{2\pi}=a$, the fraction of the circle the slice represents or $\phi_2=2a\pi+\phi_1$. So $\theta_2=\arctan [\frac ba \tan \phi_2]=2a\pi+\arctan [\frac ba \tan \phi_1]$

colormegone
  • 10,842
Ross Millikan
  • 374,822
  • I just ran through the integration myself, since it is not shown in the referenced post (so you beat me to giving the result). I edited the expressions to make it clear that the angles are not given by $\tan^{-1}(\frac{a}{b}) \cdot (\tan \theta)$ [and I was glad to see I arrived at the same answer]. – colormegone Apr 24 '13 at 20:39
  • Ack! Please don't use both subscripts and \frac in inline math. It's way too hard to read. – Josephine Moeller Apr 24 '13 at 20:42
  • Thank you for the solution and careful explanation. I'm having some trouble plugging it all in, however. Suppose a slice begins at theta1 equal to 120 degrees on the ellipse where a = 2 and b = 1. Calculating its image, phi1, according to the equation above yields -74 degrees. Is this correct, or have I made a simple mistake? – mliberatore Apr 25 '13 at 13:31
  • @cky880: the tangent is negative in the second and fourth quadrant so you need to worry about flipping through the origin. Another angle with the same tangent is $-74+180=106$ degrees, which seems reasonable. I hadn't thought about cases where it went negative and we usually take the range of arctan to be $(-90,90)$ – Ross Millikan Apr 25 '13 at 13:46
  • Ah, my mistake, thank you very much for your help! – mliberatore Apr 25 '13 at 14:03