14

A sector $P_1OP_2$ of an ellipse is given by angles $\theta_1$ and $\theta_2$.

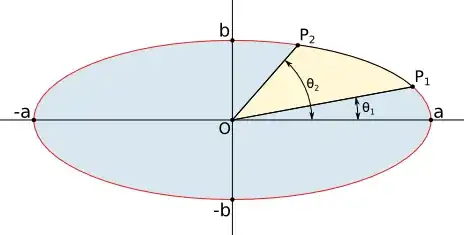
A sector of an ellipse

Could you please explain me how to find the area of a sector of an ellipse?

ezpresso
  • 593
  • 3
  • 6
  • 14

3 Answers3

10

Scale the entire figure along the $y$ direction by a factor of $a/b$. The ellipse becomes a circle of radius $a$, and the two angles become $\tan^{-1}(\frac ab\tan\theta_1)$ and $\tan^{-1}(\frac ab\tan \theta_2)$. The area of the original elliptical sector is $b/a$ times the area of the circular sector between these two angles, which is straightforward to find.

  • 3
    I think you want to multiply $y$ by a factor $\frac ab$ to make a circle, so the fractions inside the $\arctan$s should be inverted. – Ross Millikan Apr 24 '13 at 20:15
3

As I show in Evaluating $\int_a^b \frac12 r^2\ \mathrm d\theta$ to find the area of an ellipse the area of an ellipse given its central angle is:

$A(\theta) = \frac{1}{2} a b \tan ^{-1}\left(\frac{a \tan (\theta )}{b}\right)$

for $0\leq\theta\leq2\pi$, so the area of the sector in question is:

$A\left(\theta _2\right) - A\left(\theta _1\right)$

or:

$\frac{1}{2} a b \left(\tan ^{-1}\left(\frac{a \tan \left(\theta _2\right)}{b}\right)-\tan ^{-1}\left(\frac{a \tan \left(\theta _1\right)}{b}\right)\right)$

which sadly does not appear to simplify any further.

Cameron D
  • 5
-1

Using polar elliptical coordinates:$$x=a\rho cos(\theta)$$ $$y=b \rho sin(\theta)$$ the part of the plane enclosed from the ellipse is $$\{(\rho,\theta):0\le \rho \le 1,\theta\in(0,2\pi)\}$$ the Jacobian of the inverse transform is: $$J=\begin{bmatrix}a cos(\theta) & -a \rho sin(\theta) \\ b sin(\theta) & b \rho cos(\theta)\end{bmatrix}$$ so the area of a sector is: $$\int_{\theta_1}^{\theta_2}d\theta \int_0^1 d\rho a b\rho$$

Because the integral in $d\rho$ is $\frac{1}{2}ab$ the result is $$\frac{1}{2}ab(\theta_2-\theta_1)$$

Riccardo.Alestra
  • 10,546
  • 5
    I don't think this is correct. In your coordinate system, the line joining the origin to the point $(x,y) = (a\rho\cos\theta, b\rho\sin\theta)$ does not subtend an angle of $\theta$ with the $x$-axis, so your limits of integration won't be the $\theta_1$ and $\theta_2$ given in the figure. –  Feb 28 '12 at 10:37
  • 1
    No it's correct; actually this is true if $\theta_1,\theta_2$ are the eccentric angles of the corresponding points. (So it's not actually a polar coordinate system, rather a distance from centre - eccentric angle coordinate system proof.) Nice elegant rigorous proof. – Anon Sep 04 '18 at 18:58
  • The formula is incorrect for the definition of theta1 and theta2 given in the OP. I make the same mistake at https://math.stackexchange.com/a/1651008/2469 and there are other linked answers where someone makes the same mistake. –  Jun 27 '19 at 14:51
  • It is incorrect -- if it were correct, then the area from 0 to π/4 is the same as the area from π/4 to π/2, which is obviously not true. – dcromley Mar 08 '21 at 02:55