Physics undergraduate here :) I was wondering whether this is true:
The line-integral of the vector field $\vec{F}=(A,B)$ is zero for every rectangular closed path in $\mathbb{R}^2$ $\Rightarrow \vec{F}$ is conservative (it is zero around every path).
Does it actually hold?
Just in case, my "intuitition" below... :)
First, the line-integral of any smooth curve can be approximating with a "staircase" on the $(x,y)$ plane (hope it does not imply $\pi=4$): $$\int_\text{staircase} d\vec{s}\cdot\vec{F} \equiv \sum_i\left(\int_{x_i}^{x_{i+1}} A(x,y_i)dx + \int_{y_i}^{y_{i+1}} B(x_{i+1},y)dy\right)$$ $$= \sum_i\left(\int_{x_i}^{x_{i+1}} A(x,y_i)dx + \int_{y_i}^{y_{i+1}} \left[ B(x_{i},y) + O(\Delta x)\right]dy\right) $$ $$= \sum_i A(x_i,y_i)\Delta x + O(\Delta x^2) + \left[B(x_i,y_i)+O(\Delta x)\right]\Delta y + O(\Delta y^2)$$ Taking enough steps in the staircase $\Delta x \to 0 \Rightarrow \Delta y \to 0$: $$\sum_i A(x_i,y_i)\Delta x + B(x_i,y_i)\Delta y \rightarrow \int(Adx+Bdy) \equiv \int_\textrm{actual curve} d\vec{s}\cdot \vec{F}$$ And the summation over error terms vanishes: $$\sum_i O(\Delta x^2) +O(\Delta x)\Delta y + O(\Delta y^2) \sim \frac{1}{\Delta x}\times \Delta x\Delta x \to 0$$ This (hopefully) shows that the line-integral of a vector field can be approximated by a staircase. Equiped with this, we may proceed to "jusify" the claim by approximating the closed curve by many rectangular paths:
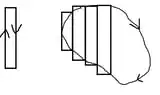
Given that the integration over every rectangle is zero by assumption and the "staircase" approximates the actual integral, the line-integral of the smooth curve is zero.
The field is conservative only if dg/dy = dh/dx.
– McCarter Jun 13 '20 at 11:31