8

I want to know the maximum and minimum absolutes values of this function:

$\ f(x,y)= 4x^2 + 9y^2 - x^2y^2 $

$\nabla f(x,y)=(8x-2xy^2,18y-2yx^2) $

I find these critical points:

$\ (0,0);(3,2);(-3,2);(3,-2);(-3;-2) $

In$\ (0,0)$ the Hessian critirium work,$\ (0,0)$ its a local minimum

But wait:

for $\ (3,2)$: $$ \begin{bmatrix} 0 & -24 \\ -24 & 0 \\ \end{bmatrix} $$

So in this case (and in the other points) the Hessian criterium doesn't work.

How I can demonstrate than $\ (0,0)$ es a absolute minimum of the function, and what about the other points? Are they saddle points? Max, Min?

Thanks very much, I'm sorry for my bad English.

Here in Argentina, the university is free, but English lessons not.

Amzoti
  • 56,093
Argentino2013
  • 147
  • 1
    Welcome to math.SE, thank you for your question. You've done a good job in asking it and showing what you've done; we will do our best to help. – vadim123 Apr 23 '13 at 02:47
  • Thanks for the welcome! Is a great site! I will try answer easy questions. – Argentino2013 Apr 23 '13 at 03:07

2 Answers2

8

Hint: Test for Extrema

Let $f$ be a function of two variables that has continuous second partial derivatives on a rectangular region $Q$ and let:

$$\displaystyle g(x,y) = f_{xx}(x, y)f_{yy}(x,y)-[f_{xy}(x,y)]^2$$

for every $(x,y)$ in $Q$.

If $(a,b)$ is in $Q$ and $f_x(a,b) = 0, f_y(a,b) = 0$, then:

  • (i) $f(a, b)$ is a local maximum of $f$ if $g(a,b) \gt 0$ and $f_{xx}(a, b) \lt 0$.
  • (ii) $f(a, b)$ is a local minimum of $f$ if $g(a,b) \gt 0$ and $f_{xx}(a, b) \gt 0$.
  • (iii) $f(a,b)$ is not an extremum of $f$ if $g(a,b) \lt 0$

We are given:

$$f(x,y)= 4x^2 + 9y^2 - x^2y^2$$

The critical points (you did great) are:

$$(0,0);(3,2);(-3,2);(3,-2);(-3,-2)$$

We have:

  • $f_x = 8x - 2xy^2, f_{xx} = 8 - 2y^2$
  • $f_y = 18y - 2x^2y, f_{yy} = 18 - 2x^2$
  • $f_{xy} = -4xy$

Now evaluate each of the critical points using the above definition.

Also, it helps to sometimes plot the function and we have:

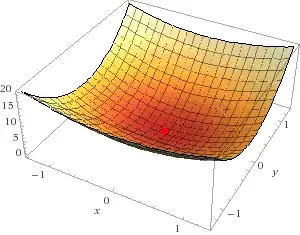
enter image description here

Examples:

  • At $(x, y) = (0, 0)$, we have $g(0,0) \gt 0$ and $f_{xx} \gt 0 \rightarrow$ a local minimum
  • At $(x, y) = (3, 2)$, we have $g(3, 2) \lt 0 \rightarrow$ not an extremum
  • Repeat for the remaining critical points

Update:

The Hessian determinant is given by:

$$\det(H) = \begin{vmatrix} f_{xx} & f_{xy} \\ f_{yx} & f_{yy}\end{vmatrix} \ $$

If you are using the Hessian, there are four conditions you need to test:

  • (01) $f_{xx} \gt 0$ and $\det H \gt 0 \rightarrow$ local minimum
  • (02) $f_{xx} \lt 0$ and $\det H \gt 0 \rightarrow$ local maximum
  • (03) $\det(H) \lt 0 \rightarrow$ saddle point
  • (04) $\det(H) = 0 \rightarrow$ no statement can be made using this approach

So, for each critical point that you found, can you now classify it using the criteria above and your approach?

Can you compare this to the approach above?

Can you look at other criteria to help distinguish the critical points as alluded to in the comments?

Amzoti
  • 56,093
  • 1
    It isn't necessarily to crank through all that: this function has four-fold symmetry, so $f(\pm3, \pm2)$ all have the same value. Also your $g(x,y)$ has the same value at all four points, since $f_{xx}$ and $f_{yy}$ are quadratic in $y$ and $x$ respectively, and $f_{xy} = \pm24$, which gets squared. – colormegone Apr 23 '13 at 03:59
  • 1
    @RecklessReckoner: Yes, and there is only one extremum at $(0,0)$ and the rest are not extremum. – Amzoti Apr 23 '13 at 04:04
  • 1
    @user73885 It may be instructive to consider "slices" through the surface at $ x = \pm 3$ and also at $ y = \pm 2$ , and similar slices nearby, to see what is strange about those critical points. – colormegone Apr 23 '13 at 04:10
  • 1
    By all means. This answer was a hint to help him have a process for classifying those critical points as we was using a Hessian approach. The hope is that he can now explore his method with this and explore the problem some more by trying different things. Regards – Amzoti Apr 23 '13 at 04:12
  • Thanks to you Amzoti and RecklessReckoner. My problem was, that I was confused with the criterium. – Argentino2013 Apr 23 '13 at 11:23
  • @user73885: Please see update for using the Hessian criteria to compare against the alternate approach provided (what do you notice about the two). regards – Amzoti Apr 23 '13 at 13:36
  • @Amzoti Check the new solution that i found with your tips – Argentino2013 Apr 23 '13 at 14:51
  • This is a wonderful answer! – Siyanda Nov 25 '13 at 06:02
0

Checking up the analysis of Amzoti, I figered out something:

$\ (3,2);(-3,2);(3,-2);(-3;-2) $ Are not extreme points.

$\ (0,0)$ Is an extreme? Lets check:

if $\ (0,0) $ is minimum, then:

$\ f(x,y) > f(0,0) $

Then

$\ f(x,0)= 4x^2 (0,0) \ is \ minimum $

$\ f(0,7)= 9y^2 (0,0) \ is \ minimum $

$\ f(x,x)= 11x^2-x^4 = h(x)$

$\ h(x)= 11x^2-x^4$

$\ h'(x)= x(22-4x^2) \\ h'(0)=0 \\ h'(\sqrt{5.5})=0 \\ h'(-\sqrt{5.5})=0 $

$\ h''(x)= 22-12x^2 \\ h''(0)= 22 $
$\ h''(\sqrt{5.5})= -44 \\ h''(-\sqrt{5.5})= -44 $

Graph of h(x)

$\ (0,0) $ is not Minimum neither maximum.

$\ f(10,10)<F(0,0) $

plot 3d of 4x^2 + 9y^2 - x^2y^2 Wolfram Alpha

Argentino2013
  • 147
  • So, we have a local minimum at $(0,0)$ for a particular region $Q$ (that were located as part of the critical points), and no global minima or maxima. Nice follow-up work to do more analysis! Sometimes the critical points allow us to get all the information we need and sometimes they can tell us nothing at all. Regards – Amzoti Apr 23 '13 at 14:55
  • yes, perfect. thanks you. – Argentino2013 Apr 23 '13 at 15:26