Find the absolute minimum and absolute maximum

Question

I have to find the absolute minimum and absolute maximum of $f(x,y) = xy$ at $D = \left \{(x,y) \in R^2: 0\leq y \leq 1-x^2 \right \}$

First I find the critical point at $\nabla f(x,y) = (y,x)$. The critical point is $(0,0)$ and $f(0,0) = 0$

I know understand that I have to look at the boundaries. This is where I have my doubts.

I know that I have $y=1-x^2$. Do I have to do $g(x)= x(1-x^2)=x-x^3$ and then $g'(x) = 1-3x^2 \Rightarrow x= \pm \sqrt{\frac{1}{3}}$ ?

I confess I'm a bit loss...

The idea is correct; your function is continuous on the compact subsect of $\mathbb R^2$ $D$; the theorem of Weierstrass guarantees the existence of abs. maxima and minima. Before moving to the boundary you should check the nature of the stationary point $(0,0)$, though. Check @Amzoti's answer for all details and this link http://math.stackexchange.com/questions/415154/lagrange-multiplier-constrain-critical-point/415285#415285 for another example — Avitus, Jun 09 '13 at 16:33

score 2 · Accepted Answer · edited Jun 09 '13 at 16:30

2

Find the absolute minimum and absolute maximum of $f(x,y) = xy$ at $D = \left \{(x,y) \in R^2: 0\leq y \leq 1-x^2 \right \}$

It is helpful to sometimes look at a plot of the function.

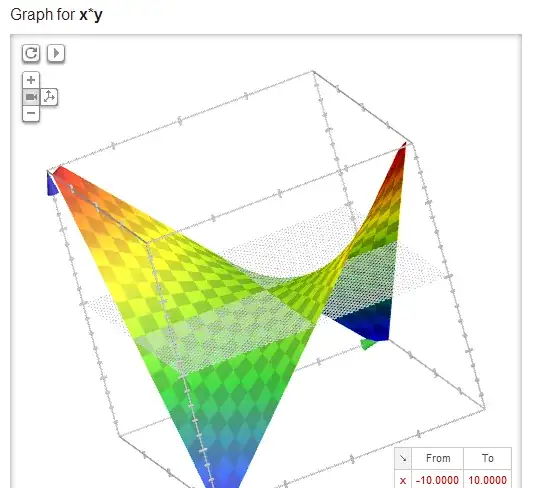
enter image description here

Critical Points:

We have $f_x = y$ and $f_y = x$, hence, we find a potential critical point at $(x, y) = (0, 0)$.

We also have $f_{xx} = f_{yy} = 0$, and $f_{xy} = f_{yx} = 1$, thus, at the critical point, we have:

$$\det(\text{Hessian}) = f_{xx}f_{yy}-f_{xy}^2 = 0 - 1 = -1$$

Since $\det(\text{Hessian}) < 0$, we have a saddle point.

Boundary:

We have $0\leq y \leq 1-x^2 $, so we see:

Finding the derivative of $x(1 - x^2)$ and equating to zero, gives us a stationary point when $x = \pm \dfrac{1}{\sqrt{3}}$

From this we have:

Absolute (global) maximum of $\dfrac{2}{3 \sqrt 3}$ at $(x, y) = \left(\dfrac{1}{\sqrt 3} , \dfrac{2}{3}\right)$
Absolute (global) minimum of -$\dfrac{2}{3 \sqrt 3}$ at $(x, y) = \left(-\dfrac{1}{\sqrt 3} , \dfrac{2}{3}\right)$

Note: you could have also used Lagrange Multipliers as an alternate approach, but I am not sure you learned that yet as well as other approaches.

edited Jun 09 '13 at 16:30

Avitus

answered Jun 09 '13 at 15:00

Amzoti

Sweet. Many thanks. I believe I now understand – Favolas Jun 09 '13 at 16:48
@Favolas: You are very welcome. I suggest that you would fill in some of the blanks by going through all of the details and comparing to your book and notes. You did great and had figured most of it out in your OP. Regards – Amzoti Jun 09 '13 at 16:54
@Amzoti : Can you tell me which software did you use to draw that nice graph?. – hrkrshnn Jun 09 '13 at 17:04
@boywholived: If you go to your search bar using google (see: http://insidesearch.blogspot.com/2012/03/graphing-on-googlecom-now-in-3d.html) and type in "plot (xy)", that is all there is to it! I would recommend learning a free CAS and there are also other wonderful (and free) tools. – Amzoti Jun 09 '13 at 17:11
awesome graph...I'm going to have to check out graphing on google! – amWhy Jun 10 '13 at 00:09
@amWhy: Check out this example - lovely! Google wants to rule the world! :-) – Amzoti Jun 10 '13 at 00:12
@Favolas: You might also want to review this entire thread - including my answer (http://math.stackexchange.com/questions/369945/maximum-and-minimum-absolute-of-a-function-x-y/369956#369956) Regards – Amzoti Jun 10 '13 at 00:14
Google will, in no time, track down, photograph, and return an image, on demand, of what any searched for human being is doing, in real time! – amWhy Jun 10 '13 at 00:15

score 0 · Answer 2 · answered Jun 09 '13 at 14:08

0

Take $y=1-x^2-z$ for some $z>0$

Then you have,

$xy=(1-x^2)x-xz$

Then you have,

$xy\ge x(1-x^2)$ if $x\le 0$(as $-xz\ge 0$)

and $xy\le x(1-x^2)$ if $x>0$(as $-xz\le 0$)

From this I guess the conclusion follows.

answered Jun 09 '13 at 14:08

Abhra Abir Kundu

2 Answers2