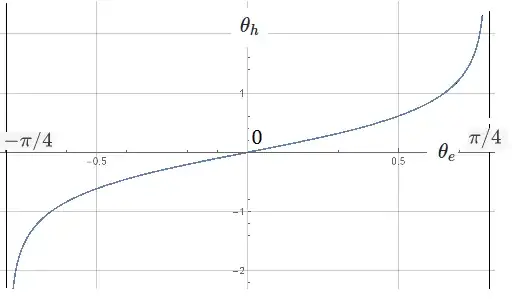Geometrical meaning is shown in the rough hand sketch:
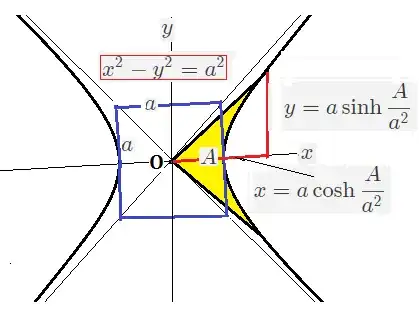
Hyperbolic angle magnitude is the non-dimensional yellow area of its hyperbolic sector marked $A$ divided by $a^2$. This is the argument of hyperbolic functions.
To get $x (y)$ co-ordinates we need to divide the area $A$ by square of axis $a,$ take its $\cosh (\sinh) $ and multiply by $a$.
EDIT1:
( This is continuation of my comments, posted here in the answer area for purpose of discussion only on OP's request.)
Why I propose using the dimensioned form:
$$ x = a \cosh \dfrac{A}{a^2};\;y = a \sinh \dfrac{A}{a^2}$$
in preference to (present day text-book model)
$$ x = \cosh A ;\;y = \sinh A \;?$$
First of all it is noted the "hyperbolic angle" is related to central polar euclidean angle $θ_e$ that the radius vector makes angle to x-axis. The hyperbolic angle is not included between any two lines.
$$ \theta_h= A/a^2 = \frac12\; \log (\tan(π/4+θ_e)):$$
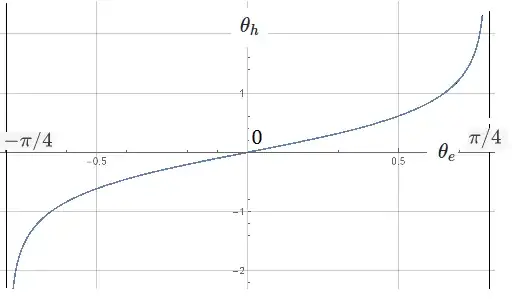
This area relation is found by direct integration.
It is difficult for me to justify full cross-validity without going into definitions of lengths and hence the dependent hyperbolic angles in any one model of the hyperbolic geometries..
My basic reasoning about its research aspect is that:
(1) Similar relations between euclidean/hyperbolic geometry should hold good for expressing cartesian coordinates in the plane using circular Trig functions and the hyperbolic functions. Subscripts $e/h$ for euclidean/hyperbolic are used as:
$$ x=a \cos θ_e,y=a \cosθ_e ;\; x=a \cosh θ_h,y=a \sinh θ_h ; $$
in either of parametrizations for:
$$ x^2 \pm y^2 = a^2 $$
(2) The sheer physical dimensional tally. I felt quite ill at ease to see $ x = \cosh A , y= \sinh A. $
(3) We cannot directly $ \cos i \theta_e \rightarrow \cosh \theta_h $ and hope to manipulate/accommodate with area interpretation.