Finding $\lim_{n\to\infty} \left(\frac{\sqrt{n^2+n}-1}{n}\right)^{2\sqrt{n^2+n}-1}$

Question

Find the following limit without using the L'Hopital rule: $$\lim_{n\to\infty} \left(\dfrac{\sqrt{n^2+n}-1}{n}\right)^{2\sqrt{n^2+n}-1}$$

Answer: $e^{-1}$

My attempt: Since the limit is of the form $1^{\infty}$, I decided to use the standard formula:

$$\lim_{x\to a} f^g = e^{\lim_\limits{x\to a}(f-1)g}$$

(See link)

Let $l=(f-1)g$.

We have, $$l=\left(\dfrac{\sqrt{n^2+n}-(1+n)}{n}\right)(2\sqrt{n^2+n}-1)$$ This on solving boils down to $$l=2n+3-\sqrt{1+\frac 1n}(2n+3)+\frac 1n$$ Now if I tend $n$ towards infinity, then $l\to 0$ and the limit i.e. $e^l$, is equal to $1$, which contradicts the given answer.

Please help. Thanks!

Edit: A proof for the "standard formula" I have used.

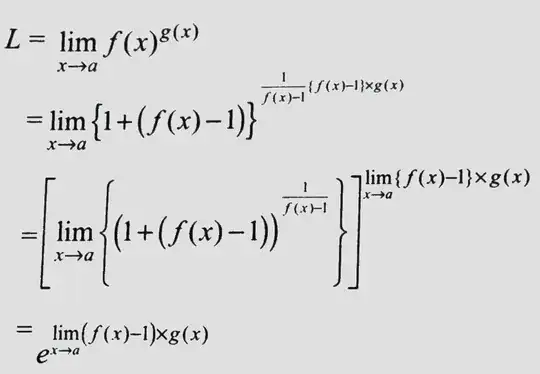
Edit 2: just noticed a typo in the power which I have now fixed.

Answer 1

$ \lim_{n \to \infty} l = -1 $, not $ 0 $. Indeed, \begin{align} 2n + 3 - \sqrt{1 + \frac{1}{n}}(2n + 3) + \frac{1}{n} &= \left(1 - \sqrt{1 + \frac{1}{n}}\right)(2n + 3) + \frac{1}{n} \\ &= \frac{(1 - \sqrt{1 + 1/n})(1 + \sqrt{1 + 1/n})}{1 + \sqrt{1 + 1/n}} \cdot (2n + 3) + \frac{1}{n} \\ &= \frac{-1/n}{1 + \sqrt{1 + 1/n}} \cdot (2n + 3) + \frac{1}{n} \\ &= - \frac{2 + 3/n}{1 + \sqrt{1 + 1/n}} + \frac{1}{n} \\ &\to -1 \end{align} as $ n \to \infty $.

Answer 2

$$a_n=\left(\frac{\sqrt{n^2+n}-1}{n}\right)^{2\sqrt{n^2+n}-1}\implies\log(a_n)=\left({2\sqrt{n^2+n}-1}\right)\log\left(\frac{\sqrt{n^2+n}-1}{n}\right)$$ Now, using Taylor expansions $$\log\left(\frac{\sqrt{n^2+n}-1}{n}\right)=-\frac{1}{2 n}-\frac{1}{4 n^2}-\frac{1}{24 n^3}+O\left(\frac{1}{n^4}\right)$$ $${2\sqrt{n^2+n}-1}=2 n-\frac{1}{4 n}+\frac{1}{8 n^2}-\frac{5}{64 n^3}+O\left(\frac{1}{n^4}\right)$$ $$\log(a_n)=-1-\frac{1}{2 n}+\frac{1}{24 n^2}+O\left(\frac{1}{n^3}\right)$$ $$a_n=e^{\log(a_n)}=\frac 1e \left(1-\frac{1}{2 n}+\frac{1}{6 n^2} \right)+O\left(\frac{1}{n^3}\right)$$ which shows the limit and how it is approached.

Moreover, this gives a shortcut estimation of $a_n$. Suppose $n=10$ $$a_{10}=\left(\frac{10}{\sqrt{110}-1}\right)^{1-2 \sqrt{110}}\approx 0.350040$$ while the truncated expansion gives $\frac{571}{600 e} \approx 0.350099$.

Answer 3

You can also do it by asymptotics. Indeed, using $\sqrt{1+1/n}= 1 + \frac{1}{2n} + \mathcal{O}(1/n^2)$ as $n\to\infty$. Your expression then simplifies as follows, $$\left(\frac{n\sqrt{1+1/n} - 1 }{n}\right)^{2n\sqrt{1+1/n} -1} = \left(1-\frac{1}{2n} + \mathcal{O}(1/n^2) \right)^{2n+\mathcal{O}(1/n)}\qquad \text{as } n\to\infty.$$ By using $a_n^{b_n} = e^{b_n\log a_n}$, the expression can be simplified to $e^{-1+\mathcal{O}(1/n)}= e^{-1}+\mathcal{O}(1/n)$. Hence the limit is $e^{-1}$.